概念
对于有根树 $T$ 的两个结点 $u,v$,它们的最近公共祖先(Lowest Common Ancestors)表示一个结点 $x$,满足 $x$ 是 $u$ 和 $v$ 的祖先且 $x$ 的深度尽可能大。在这里,一个节点也可以是它自己的祖先。
LCA 可以求树上两个节点之间的最短路径。$dis(u,v)$ 其实就是 $u\to \text{lca}(u,v)\to v$。
写的是模板是因为一道题都没做出来。以后会补树上差分(
倍增 这应该是最好理解的一种方法。
首先我们要知道暴力求 LCA 的方法:
先把深度较大的那个节点往上跳,直到与另一个节点深度相同。
两个节点同时往上跳,直到两节点重合。这个重合的位置就是它们的 LCA。
其实倍增的基本思路也是这个样子,但是与暴力不同的是,上述方法在节点往上跳的时候,是不断跳到它的父节点,也就是一个一个跳的。但是,为了追求速度,倍增 LCA 并没有一个一个地跳。
不知道大家还记得二进制拆分吗?任何一个整数,都可以拆成若干个 $2$ 的幂次相加的形式,且这些幂次互不相同。倍增 LCA 的思路也是这样的:任意一个节点到它 LCA 的距离肯定都是整数,所以一定可以拆出若干个互不相同的 $2$ 的幂次使得这些数的和是它。
以第二步为例,我们可以从大到小 枚举 $k$:如果这两个节点往上跳 $2^k$ 之后还不能重合,那就说明 LCA 到它们的距离大于 $2^k$,跳上去了之后也不会错过 LCA,我们就直接把两个节点跳上去,然后接着枚举,直到两个节点可以重合。这个过程复杂度是 $\Theta(\log n)$。
第一步也是类似的,倍增地往上跳,直到两节点深度相同为止。
于是思路就想明白了。但是我们在往上跳的时候必须知道两个节点往上跳了一个距离之后会不会重合。所以需要预处理一下:$dp_{i,j}$ 代表 $i$ 节点上面的第 $2^j$ 个节点的编号。比如 $dp_{i,0}$ 就代表的是 $i$ 的父节点。
如何求解 $dp$ 数组呢?预处理打一个 DFS,有两个用处:
求解每一个节点的深度。
求 $dp$ 数组。
往下枚举的时候,我们知道一个节点的父节点是谁,实现起来传个参就行。假设 $v$ 的父节点是 $u$,那么先可以知道 $dp_{v,0}=u$。接着,用这个条件求出:$dp_{v,1}=dp_{u,0}$,也就是 $u$ 的父节点,假设这个节点是 $r$。然后就可以再求出:$dp_{v,2}=dp_{u,1}=dp_{r,0}$……推出通用的式子就是:
这应该相当于是一个树形 DP。
使用这个数组就很简单了,判断 $u,v$ 往上跳 $2^k$ 会不会重合就是判断 $dp_{u,k}$ 是否等于 $dp_{v,k}$。
参考代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 #include <cstdio> #include <vector> #include <cmath> #define rep(i, j, k) for(int i = j; i <= k; ++i) #define dep(i, j, k) for(int i = j; i >= k; --i) const int maxn = (int )2e4 + 5 ;std::vector<int > G[maxn]; int n, m, l, dep[maxn], dp[maxn][305 ];bool vis[maxn];inline void swap (int &x, int &y) inline int LOG2F (int x) return (int )log2 (x); } void dfs (int u, int fa) int len = G[u].size () - 1 ; rep (i, 0 , len) { int v = G[u][i]; if (v != fa) { dep[v] = dep[u] + 1 ; dp[v][0 ] = u; rep (k, 1 , l) dp[v][k] = dp[dp[v][k - 1 ]][k - 1 ]; dfs (v, u); } } return ; } inline int getLCA (int x, int y) if (dep[x] < dep[y]) swap (x, y); while (dep[x] > dep[y]) x = dp[x][LOG2F (dep[x] - dep[y])]; if (x == y) return x; dep (k, LOG2F (dep[x]), 0 ) if (dp[x][k] != dp[y][k]) x = dp[x][k], y = dp[y][k]; return dp[x][0 ]; } int main () int root = 1 ; scanf ("%d" , &n); l = LOG2F (n); int a, b, c; rep (i, 1 , n) { scanf ("%d:(%d)" , &a, &b); rep (i, 1 , b) { scanf ("%d" , &c); vis[c] = 1 ; G[a].push_back (c); G[c].push_back (a); } } rep (i, 1 , n) { if (!vis[i]) { root = i; break ; } } dep[root] = 1 ; dfs (root, 0 ); scanf ("%d" , &m); rep (i, 1 , m) { scanf ("%d %d" , &a, &b); printf ("%d\n" , getLCA (a, b)); } return 0 ; }
Tarjan LCA Tarjan 是一个人,他提出了很多牛逼的算法,比如说这个求 LCA 的算法,它可以在线性时间复杂度内求解若干个 LCA 的询问。当然,速度快是有代价的,Tarjan LCA 是离线算法,如果有强制在线就用不了了……
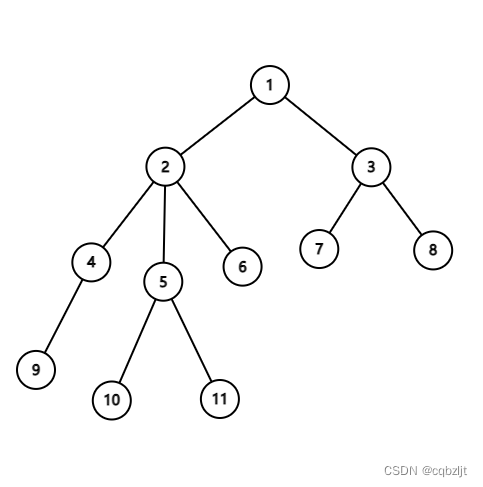
如果大家模拟过 DFS 一棵树的过程,就会发现,任意两个节点之间,DFS 遍历的路径肯定是这两个节点之间的最短路径!比如这个树:
它的遍历顺序就应该是:
1 1 2 4 9 4 2 5 10 5 11 5 2 6 2 1 3 7 3 8 3 1
这个东西也就是我们说的欧拉序 。
知道了最短路径其实也就知道 LCA 了,因为最短路径肯定经过 LCA。假如说我想求 $10$ 和 $6$ 的 LCA,我们就把第一个 $10$ 到第一个 $6$ 这一段截取出来(其实是第几个都无所谓,反正中间也不会出现比 $\text{lca}$ 深度更小的节点),也就是:
发现这一段深度最小的是节点是 $2$。所以 $\text{lca}(6,10)$ 就是 $2$。
这个思路衍生出了两种方法,第一种就是直接求用 ST 表求最小值,也就是下面介绍的第三种方法。但是 Tarjan 一看,不行,ST 表时间复杂度太大了,还有一种更快的办法。
我们一边 DFS,一边建立并查集 ,首先所有的待求节点都在不同的集合里。接着我们用一个数组 $col$ 代表这个节点有没有被遍历过。DFS 函数在遍历节点 $u$ 的时候都干了三件事:
枚举 $u$ 所有子节点 $v$。每次先沿着 $v$ DFS 下去,然后再把 $v$ 所在的集合改为 $u$ 的集合。
标记 $u$ 已经被走过。
枚举所有询问,如果发现有某些组的询问一个节点是 $u$,另一个节点已经被遍历过 ,那这两个节点的 LCA 就是不是 $u$ 的那个点 所在并查集的根。
如何证明算法正确性?首先,遍历到 $u$ 的时候,被标记的节点一定不是 $u$ 的祖先节点,因为 $u$ 的祖先节点都没有回溯回去,不可能被标记。于是我们就知道了 $v$ 不可能是 $\text{lca}(u,v)$。其次,对于任意一个节点,总会先 DFS 下去,等回溯回来之后再让它加入其父节点的集合,所以,因为遍历过来的路程有一部分是 $v\to\text{lca}(u,v)\to u$,$v\to \text{lca}(u,v)$ 这一段所有节点都已经从下到上加入其父节点的集合,但是,从 $\text{lca}(u,v)$ 的父节点开始一直往上走到根节点那一段没有回溯回来,也就没有进行关于并查集的操作,所以 $v$ 所在集合的根节点显然就是在此集合中深度最小的 $\text{lca}(u,v)$。
参考代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 #include <cstdio> #include <vector> #define rep(i, j, k) for(int i = j; i <= k; ++i) #define dep(i, j, k) for(int i = j; i >= k; --i) const int maxn = (int )5e6 + 5 ;int n, q, ans[maxn];std::vector<int > G[maxn], Q[maxn], Q_id[maxn]; bool col[maxn];int fa[maxn];inline int findset (int x) return x == fa[x] ? x : fa[x] = findset (fa[x]); }void tarjan (int u, int dad) int len = G[u].size () - 1 ; rep (i, 0 , len) { if (G[u][i] != dad) { tarjan (G[u][i], u); fa[G[u][i]] = u; } } col[u] = 1 ; len = Q[u].size () - 1 ; rep (i, 0 , len) { if (col[Q[u][i]]) ans[Q_id[u][i]] = findset (Q[u][i]); } return ; } int main () scanf ("%d %d" , &n, &q); rep (i, 1 , n) fa[i] = i; int u, v; rep (i, 1 , n - 1 ) { scanf ("%d %d" , &u, &v); G[u].push_back (v); G[v].push_back (u); } rep (i, 1 , q) { scanf ("%d %d" , &u, &v); Q[u].push_back (v), Q_id[u].push_back (i); Q[v].push_back (u), Q_id[v].push_back (i); } tarjan (1 , 0 ); rep (i, 1 , q) printf ("%d\n" , ans[i]); return 0 ; }
欧拉序 + ST 表 思路在上面讲过了。可以开一个数组 $pos$ 来记录每一个节点在 dfs 序中第一次出现的下标,这样就可以把求 $\text{lca}(u,v)$ 转换为求 $[pos_u,pos_v]$ 这一段深度最小的节点的权值。ST 表的实现可以使用结构体。
参考代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 #include <cstdio> #include <vector> #include <cmath> #include <cctype> #define rep(i, j, k) for(int i = j; i <= k; ++i) #define dep(i, j, k) for(int i = j; i >= k; --i) const int maxn = (int )1e6 + 5 ;int n, q, root = 1 , tot, dep[maxn], pos[maxn], dfn[maxn], ddep[maxn];std::vector<int > G[maxn]; inline int read () int x = 0 , w = 0 ; char ch = 0 ; while (!isdigit (ch)) { w |= ch == '-' ; ch = getchar (); } while (isdigit (ch)) { x = (x << 3 ) + (x << 1 ) + (ch ^ 48 ); ch = getchar (); } return w ? -x : x; } inline void write (int x) if (x < 0 ) putchar ('-' ), x = -x; if (x > 9 ) write (x / 10 ); putchar (x % 10 + '0' ); } struct RMQ { int num, id; friend bool operator <(RMQ x, RMQ y) { return x.num < y.num; } } dp[maxn][35 ]; inline RMQ min (RMQ x, RMQ y) return x < y ? x : y; }inline void init () rep (i, 1 , tot) dp[i][0 ].num = ddep[i], dp[i][0 ].id = dfn[i]; for (int j = 1 ; 1 << j <= tot; ++j) for (int i = 1 ; i + (1 << (j - 1 )) - 1 <= tot; ++i) dp[i][j] = min (dp[i][j - 1 ], dp[i + (1 << (j - 1 ))][j - 1 ]); return ; } inline RMQ rmq (int L, int R) if (L > R) L ^= R, R ^= L, L ^= R; int k = (int )log2 (R - L + 1 ); return min (dp[L][k], dp[R - (1 << k) + 1 ][k]); } void dfs (int u, int fa) int len = G[u].size () - 1 ; dfn[++tot] = u; pos[u] = tot; rep (i, 0 , len) { int v = G[u][i]; if (v != fa) { dep[v] = dep[u] + 1 ; dfs (v, u); dfn[++tot] = u; } } return ; } int main () n = read (), q = read (); int x, y, ans = 0 ; rep (i, 1 , n - 1 ) { x = read (), y = read (); G[x].push_back (y); G[y].push_back (x); } dfs (root, 0 ); rep (i, 1 , tot) ddep[i] = dep[dfn[i]]; init (); rep (i, 1 , q) { x = read (), y = read (); ans = rmq (pos[x ^ ans], pos[y ^ ans]).id; write (ans); putchar ('\n' ); } return 0 ; }
树链剖分 其实树剖求 LCA 思路跟倍增有点像,都是往上跳到 LCA 为止。但是两种方法的跳法不一样:倍增是利用二进制原理精准找到 LCA 的位置,树剖则是跳重链,直到两个节点在一条重链上。
在阅读以下内容之前,请确保您理解了关于树剖的基础内容 (概念及两个 DFS 函数)。
执行的操作也就是这样的,不断重复:
判断 $u,v$ 是否在一条重链上:
若是,返回 $u,v$ 当中深度较小的那个节点。
若不是,就比较两个节点所在重链的链头的深度 ,把深度较大的那个节点跳到其重链链头的父节点。
为什么不是直接比较两个节点的深度,而是要比较两个节点所在重链链头的深度呢?因为节点跳是跳到链头父节点,所以如果直接比较两节点深度,有可能跳上去了之后会错过 LCA。另外,跳到链头父节点的原因是需要换一条重链。
参考代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 #include <cstdio> #include <vector> #include <cmath> #define rep(i, j, k) for(int i = j; i <= k; ++i) #define dep(i, j, k) for(int i = j; i >= k; --i) const int maxn = (int )1e5 + 5 ;std::vector<int > G[maxn]; int n, m, dep[maxn], ft[maxn], sum[maxn], son[maxn], top[maxn];void dfs1 (int u, int fa) ft[u] = fa; int len = G[u].size () - 1 , mx = 0 ; rep (i, 0 , len) { int v = G[u][i]; if (v != fa) { dep[v] = dep[u] + 1 ; dfs1 (v, u); sum[u] += sum[v]; if (sum[v] > mx) { mx = sum[v]; son[u] = v; } } } ++sum[u]; return ; } void dfs2 (int u, int fa, int tp) top[u] = tp; int len = G[u].size () - 1 ; rep (i, 0 , len) { int v = G[u][i]; if (v != fa) { if (v == son[u]) dfs2 (v, u, tp); else dfs2 (v, u, v); } } return ; } inline int getLCA (int x, int y) while (top[x] != top[y]) { if (dep[top[x]] < dep[top[y]]) y = ft[top[y]]; else x = ft[top[x]]; } return dep[x] < dep[y] ? x : y; } inline int dis (int x, int y) return dep[x] + dep[y] - (dep[getLCA (x, y)] << 1 ); }int main () scanf ("%d" , &n); int a, b; rep (i, 1 , n - 1 ) { scanf ("%d %d" , &a, &b); G[a].push_back (b); G[b].push_back (a); } dfs1 (1 , 0 ); dfs2 (1 , 0 , 1 ); scanf ("%d" , &m); rep (i, 1 , m) { scanf ("%d %d" , &a, &b); if (a == b) printf ("0\n" ); else printf ("%d\n" , dis (a, b)); } return 0 ; }
对比 设树有 $n$ 个节点,询问 $q$ 次,四种算法对比如下:
倍增
tarjan
DFS 序 + ST 表
树链剖分
时间复杂度 $\Theta((n+q)\log n)$
$\Theta(n+q)$
$\Theta(n+q+n\log n)$
$\Theta(2n+q\log n)$
离线/在线 在线
离线
在线
在线
(表格 From mjl 的 PPT)
可以发现,tarjan 的方法速度是最快的,所以在允许离线的时候建议使用,树剖的速度名列第二,如果需要在线的话它是最好的选择。