前置芝士

概念 & 性质

处理一棵树会比较棘手，但是如果我们有办法把这棵树处理成一条一条的链，那就好解决多了。

树链剖分，简称树剖，就是干的这事。树链剖分有两种方法：重链剖分和长链剖分。因为长链剖分不常用，所以这一篇介绍的的都是重链剖分。

在了解接下来的内容之前，先要了解几个概念。

  • 重儿子：每个子树中，子树大小（即子树包含节点数）最大的子节点
  • 轻儿子：除重儿子外的其他子节点
  • 重边：每个节点与其重儿子间的边
  • 轻边：每个节点与其轻儿子间的边
  • 重链：重边连成的链
  • 轻链：轻边连成的链

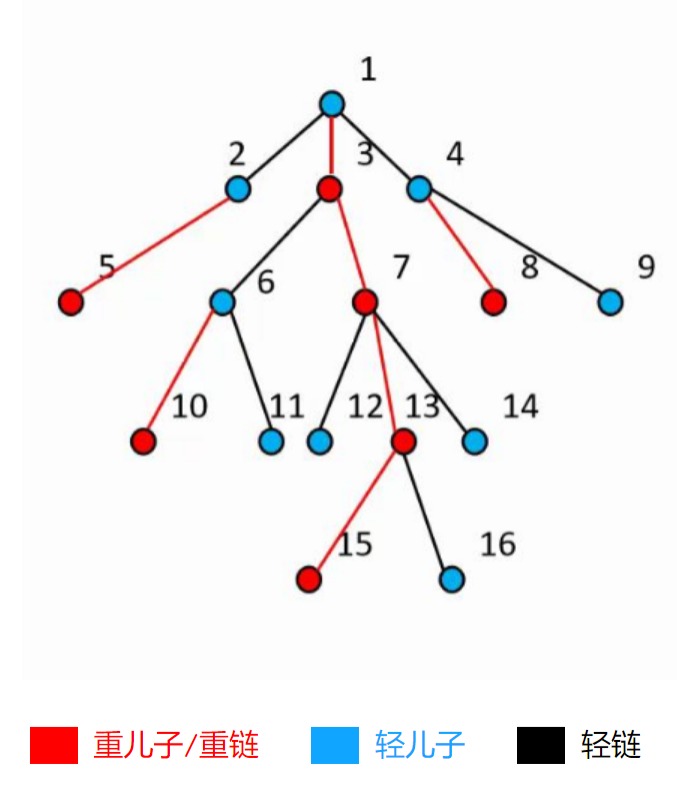
大家发现没有，这里有三组相对的概念。为了更好的理解这几个概念，让我们在 mjl 的 PPT 上白嫖一棵树过来：

因为单独一个节点也可以看作重链，所以这棵树上的重链分布如下：

颜色标出来应该就很清晰了，每一条重链的链头都是轻儿子，后面全部都是重儿子。

因为 Hexo 对 $\LaTeX$ 的支持很不友好，所以窝直接从 luogu 的博客上截图截下来了 qwq。

除了上面说的，重链还有几个性质：

  1. 每一个节点只能在一条重链上，而且必定在重链上。（原因：每个节点只有一个重儿子。）
  2. 一个点到根节点的路径上最有只有 $\log n$ 条轻边。（原因：若 $v$ 为 $u$ 子节点且 $(u,v)$ 为轻边，则子树大小 $2sum_v\le sum_u$。）

树链剖分の基本解法

两个 DFS 预处理

既然每一条重链的头都是轻儿子，我们可以通过标记每一个节点所在重链的链头节点的方法来存储重链。在此之前，我们要开几个数组：

  • $ft_u$: $u$ 的父节点；根节点 $ft_1=0$
  • $dep_u$: $u$ 节点的深度
  • $sum_u$: 以 $u$ 为根节点的子树的大小
  • $son_u$: $u$ 的重儿子；叶子节点 $son_u=0$
  • $top_u$: $u$ 所在重链的链头节点

第一个 DFS 需要做以下事情：

  1. 初始化每一个节点的父节点 $ft$，深度 $dep$ 和子树大小 $sum$；
  2. 求出每一个非叶子节点的重儿子 $son$。

代码长这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void dfs1(int u, int fa) { // u 为遍历到的节点，fa 为 u 的父节点
    ft[u] = fa; // 初始化 ft 数组
    int len = G[u].size() - 1, mx = 0; // mx 存 u 的儿子中子树大小的最大值
    rep(i, 0, len) { // 遍历 u 的子节点
        int v = G[u][i];
        if(v != fa) {
            dep[v] = dep[u] + 1; // 初始化 dep 数组，是父亲向儿子转移，记得写在 dfs 的前面
            dfs1(v, u);
            sum[u] += sum[v]; // 累加 u 的子树大小
            if(sum[v] > mx) { // 判断重儿子
                mx = sum[v]; // 更新最大子树大小
                son[u] = v; // 更新 u 的重儿子
            }
        }
    }
    ++sum[u]; // 别忘了把 u 自己加上
    return;
}

第二个 DFS 的任务很简单：

  1. 算出 $top$ 数组。
  2. （可选）如果后面需要用 dfs 序（可能性很大）也需要求一下。

代码长这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void dfs2(int u, int fa, int tp) { // u、fa 含义同上，tp 为目前重链的链头
    top[u] = tp; // 初始化 top 数组
    dfn[++tot] = w[u]; // 求 dfs 序
    id[u] = tot; // 存一下每一个节点在 dfs 序中出现的位置
    int len = G[u].size() - 1;
    if(son[u]) // 先搜重儿子
        dfs2(son[u], u, tp); // 重链还是那一根，所以链头不变
    rep(i, 0, len) { // 搜轻儿子
        int v = G[u][i];
        if(v != fa && v != son[u])
            dfs2(v, u, v); // 换了一根重链，轻儿子做链头
    }
    return;
}

这个代码遗留了两个问题：

  1. 为什么 dfs 序只需要加一次节点？

    A：其实加一次或者两次两种写法都是对的，加一遍会更方便，两遍对于子树的更新思考起来比较好想出来，下文讲解使用加一遍的方法，两种写法的代码都有，供参考。

  2. 为啥要先搜重儿子？

    A：为了让 dfs 序中每一条重链都连在一起，重儿子之间没有轻儿子捣乱，方便后面跳重链的时候用线段树维护。

树链剖分の妙用

1. 求 LCA

详情请见 LCA 文章中的树剖解法。

2. 在树上维护线段树

利用树剖把树转换为线性的链的特征，结合 dfs 序，可以利用树剖在树上维护线段树，从而达到一些目的。

例题：【模板】树链剖分/轻重链剖分

要求维护的操作是两点之间的简单路径和子树的修改与查询，很明显可以用 dfs 序把树转换为数组再用线段树维护。

首先子树比较好操作，因为 dfs 序中子树是连在一起的，故以 $u$ 为根节点的子树在 dfs 序中的范围就是 $[id_u,id_u+sum_u-1]$，用区间修改、区间查询的线段树维护即可。

维护两节点之间的简单路径需要参考求 LCA 的方法，因为 $u,v$ 跳上去的路径就是这条简单路径。由于 $u,v$ 在跳到一条重链上之前都是一条一条跳重链，所以我们可以一边跳一边用线段树维护这些重链。最后两节点到一条重链上之后，再维护两节点之间的区间即可。我们生成 dfs 序的规则保证了这些区间都是连续的。

代码还挺难打的，我调了一个上午/kk。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
/**
 * @file P3384.cpp
 * @author Liynw
 * @brief 树链剖分（轻重链剖分）模板
 * @date 2022-05-03
 * 
 * @copyright Copyright (c) 2022
 * 
 */
#include <cstdio>
#include <vector>
#define int long long
#define rep(i, j, k) for(int i = j; i <= k; ++i)

const int maxn = (int)1e6 + 5;

int n, q, r, mod, tot, w[maxn], ft[maxn], son[maxn], sum[maxn], dep[maxn], top[maxn], id[maxn], dfn[maxn << 1];
std::vector<int> G[maxn];

namespace Segment_Tree {

struct _ {
    int val, target, len;
} t[maxn << 2];

inline void swap(int &x, int &y) { x ^= y, y ^= x, x ^= y; }

void build(int p, int l, int r) {
    t[p].len = r - l + 1;
    if(l == r) {
        t[p].val = dfn[l];
        return;
    }
    int lc = p << 1, rc = p << 1 | 1, mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    t[p].val = t[lc].val + t[rc].val;
    return;
}

inline void pushdown(int p) {
    int l = p << 1, r = p << 1 | 1;
    t[l].val += t[l].len * t[p].target;
    t[r].val += t[r].len * t[p].target;
    t[l].target += t[p].target;
    t[r].target += t[p].target;
    t[p].target = 0;
    return;
}

void update(int p, int l, int r, int L, int R, int k) {
    if(L <= l && r <= R) {
        t[p].val += t[p].len * k;
        t[p].target += k;
        return;
    }
    pushdown(p);
    int lc = p << 1, rc = p << 1 | 1, mid = (l + r) >> 1;
    if(L <= mid)
        update(lc, l, mid, L, R, k);
    if(R > mid)
        update(rc, mid + 1, r, L, R, k);
    t[p].val = t[lc].val + t[rc].val;
    return;
}

int query(int p, int l, int r, int L, int R) {
    if(L <= l && r <= R)
        return t[p].val;
    pushdown(p);
    int lc = p << 1, rc = p << 1 | 1, mid = (l + r) >> 1, sum = 0;
    if(L <= mid)
        sum += query(lc, l, mid, L, R);
    if(R > mid)
        sum += query(rc, mid + 1, r, L, R);
    return sum;
}

}
using namespace Segment_Tree;

void dfs1(int u, int fa) {
    ft[u] = fa;
    int len = G[u].size() - 1, mx = 0;
    rep(i, 0, len) {
        int v = G[u][i];
        if(v != fa) {
            dep[v] = dep[u] + 1;
            dfs1(v, u);
            sum[u] += sum[v];
            if(sum[v] > mx) {
                mx = sum[v];
                son[u] = v;
            }
        }
    }
    ++sum[u];
    return;
}

void dfs2(int u, int fa, int tp) {
    top[u] = tp;
    dfn[++tot] = w[u];
    id[u] = tot;
    int len = G[u].size() - 1;
    if(son[u]) {
        dfs2(son[u], u, tp);
    }
    rep(i, 0, len) {
        int v = G[u][i];
        if(v != fa && v != son[u])
            dfs2(v, u, v);
    }
    return;
}

inline void Update(int u, int v, int x) {
    while(top[u] != top[v]) {
        if(dep[top[u]] < dep[top[v]])
            swap(u, v);
        update(1, 1, tot, id[top[u]], id[u], x);
        u = ft[top[u]];
    }
    if(dep[u] > dep[v])
        swap(u, v);
    update(1, 1, tot, id[u], id[v], x);
    return;
}

inline int Query(int u, int v) {
    int s = 0;
    while(top[u] != top[v]) {
        if(dep[top[u]] < dep[top[v]])
            swap(u, v);
        s += query(1, 1, tot, id[top[u]], id[u]);
        u = ft[top[u]];
    }
    if(dep[u] > dep[v])
        swap(u, v);
    return s + query(1, 1, tot, id[u], id[v]);
}

signed main() {
    scanf("%lld %lld %lld %lld", &n, &q, &r, &mod);
    rep(i, 1, n)
        scanf("%lld", &w[i]);
    int u, v;
    rep(i, 2, n) {
        scanf("%lld %lld", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    dfs1(r, 0);
    dfs2(r, 0, r);
    build(1, 1, tot);
    int op, x, y, z;
    rep(i, 1, q) {
        scanf("%lld", &op);
        if(op == 1) {
            scanf("%lld %lld %lld", &x, &y, &z);
            Update(x, y, z);
        } else if(op == 2) {
            scanf("%lld %lld", &x, &y);
            printf("%lld\n", Query(x, y) % mod);
        } else if(op == 3) {
            scanf("%lld %lld", &x, &y);
            update(1, 1, tot, id[x], id[x] + sum[x] - 1, y);
        } else {
            scanf("%lld", &x);
            printf("%lld\n", query(1, 1, tot, id[x], id[x] + sum[x] - 1) % mod);
        }
    }
    return 0;
}

变式：

  • 「ZJOI2008」树的统计

    这个题目应该比板子简单，甚至都不需要区间修改，线段树维护一个结构体即可。敲代码的时候注意：

    1. 注意检查线段树有没有挂。
    2. 节点权值有可能是负数。所以记得求最大值的时候把初始值赋为极小值。
    3. 打线段树的时候可以巧用运算符重载，比如我是这么写的： 
      1
      2
      3
      4
      struct _ {
          int s, m;
          _ operator+(const _ &x) const { return (_) { s + x.s, max(m, x.m) }; }
      } t[maxn << 2], empty;

  • 「HAOI2015」树上操作

    几乎和模板一样，只是查询多了一个到根节点的询问，这个函数传参变一下就行了。当然，如果明确知道其中一个节点是根节点，树链剖分也可以这么写：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    inline void Update(int x, int k) {
        while(x) { // 直接跳 x 即可，不用考虑根节点
            update(1, 1, tot, id[top[x]], id[x], k);
            x = ft[top[x]];
        }
        return;
    }
      
    inline int Query(int x) {
        int s = 0;
        while(x) {
            s += query(1, 1, tot, id[top[x]], id[x]);
            x = ft[top[x]];
        }
        return s;
    }

    啊对了，这题数组要开 1e6 而非 1e5，不然只有 $30$ 分，望周知。

  • 「NOI2015」软件包管理器

    也是板子，不过需要一个转化。

    最开始是一棵初始值全部为 $0$ 的树。

    install 操作：判断 $0\to u$ 路径上有多少个 $0$，并全部改为 $1$。可以再次转换：因为点权只有 $0/1$，故查询操作就是求 $dep_u-\text{query}(1\to u)$。

    uninstall 操作：判断 $u$ 的子树上有多少个 $1$，并全部改为 $0$。