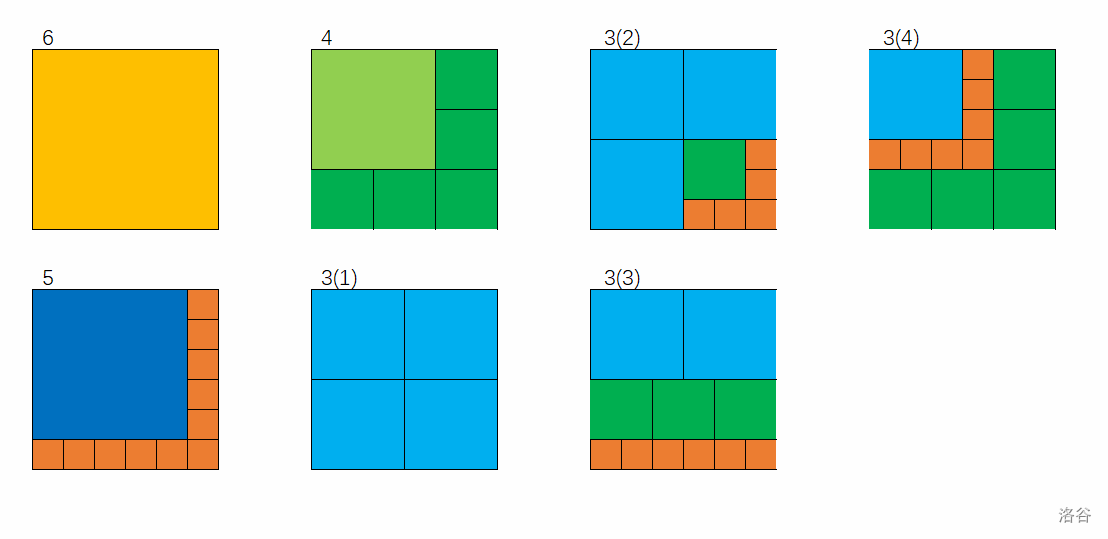打包装箱 题解

Update on 2021/10/1：修复了 $\LaTeX$ 格式。

1.题目

题目描述

学校组织了爱心捐书活动，同学们纷纷踊跃把自己看过的旧书拿出来捐给贫困山区的孩子们。图书室的马老师把同学们捐献的书打包在了6种纸箱子里（打包好的各类纸箱子有若干个），纸箱子的高相同，但底面积分为 $1\times 1$，$2\times 2$，$3\times 3$，$4\times 4$，$5\times 5$，$6\times 6$。现为了装车方便，需要把这些纸箱子装在若干个 $6\times 6$ 的木箱子，木箱子的高和打包纸箱子相同，请你帮助马老师，用最少的木箱子打包完所有的纸箱子。

输入

一行（六个数）用空格隔开，分别表示 $1\times 1$，$2\times 2$，$3\times 3$，$4\times 4$，$5\times 5$，$6\times 6$ 六类纸箱子的个数（每类箱子的个数小于等于 $100$）。

输出

一行，最少的木箱子个数

样例输入

1	6 5 4 3 2 1

样例输出

~~是的，为了我们“亲爱”的mjl，我把题目改了（（~~

2.算法分析

用最少的木箱子装完，也就是说让剩余的空间最小，最好的情况就是除了最后一个箱子，其他箱子都装满，所以只需要考虑箱子内部的情况。故这道题可以用贪心算法解决。

3.思路

要解决箱子内部如何装满的问题，我们首先需要根据题目条件建立模型。题目告诉我们有六种不同的纸箱子和木箱子的大小，根据这些条件我们可以列出箱子内部装满时的模型如下（PS：最上面的那个数字指的是最大的那个纸箱子）：

装进去的情况

可以看出，在纸箱子的大小为 $3\times 3$ 时，情况比较多比较复杂，所以需要着重考虑。

需要注意的是，在装箱的时候我们会优先把所有 $3\times 3$ 的纸箱子装到一个木箱子里（即 $4$ 个 $3\times 3$ 的箱子装在一个木箱子里），所以剩下的那三种情况只需要判断一次。（我就是在这个地方栽的）

这里再补充两个编程的技巧（不想看请跳过）：

（1）向上取整

如果一个人问大家怎么向上取整的话，估计大多数人的回答应该都是用 <cmath> 头文件里的 ceil 函数。但是这多少有点麻烦，~~如果你懒得写~~为了方便，其实根本不需要什么函数，用整数除法就可以实现。

在 c++ 中，整数的除法是默认为向下取整。我们假设 $n$ 可以被 $k$ 整除且 $n/k=q$，那么：

$(n+1)/k=q$

$(n+2)/k=q$

$……$

$(n+k-1)/k=q$

$(n+k)/k=q+1$

由此可以看出，如果我们要向上取整一个除法 $n/k$ （余数为 $r$ ），就需要把 $n$ 的范围提到 $n+(k-r)$ 到 $n+(k-r)+(k-1)$ 这个范围之内，而当这个被除数的加数取到 $k-1$ 的时候，不管余数怎么变，被除数永远都在这个范围。综上所述，向上取整的公式为：

$\lceil n/k \rceil=(n+k-1)/k$

（2）辅助数组——为“偷懒”而生

在数的计算中，我们通常要根据结果的不同而使用不同的值。这个问题可以用条件选择语句解决，但是当情况太多的时候就会造成程序的内容繁杂。（而且写着也麻烦！）当一个计算结果与一个值可以一一对应的时候，我们就可以用辅助数组简化程序。

（注：如果数与值不是一一对应的，也可以使用辅助数组，但是一定是一个值对应一个结果（也就是说不同的结果可以对应同一个值），但是~~在本人的学习范围之内~~辅助数组不能同一个结果对应多个值。）

拿这道题举例，由于 $3\times 3$ 纸箱子的个数不一定能被 $4$ 整除，这也就意味着当个数除以 $4$ 的时候余数可能是 $0,1,2,3$，不同的值对应边长为 $2\times 2$的纸箱子在放有这些剩余的 $3\times 3$ 的箱子的木箱子中能放得下的不同个数，计算的结果与值一一对应。所以我们可以设置一个辅助数组 cnt，从 $0$ 到 $3$ 号位分别存储余数为 $0,1,2,3$ 的不同情况所对应的值，这样我们在使用这个值的时候就可以直接调用数组，不用写条件语句。

4.编写代码

终于到了激动人心的时刻了!

AC 代码（不要复制，~~但你要复制我也没办法~~）：

#include<cstdio>
int cnt[4]={0,5,3,1};//辅助数组
int main(){
    int a1,a2,a3,a4,a5,a6,sum=0,x,y;
    scanf("%d %d %d %d %d %d",&a1,&a2,&a3,&a4,&a5,&a6);
      //边长为6，5，4，3的盒子需要的箱子数  
    sum=a6+a5+a4+(a3+3)/4;
      //边长为2的盒子在已经装了的箱子中可以装的数量     
    x=a4*5+a3*cnt[a3%4];              
    if(x<a2)sum+=(a2-x+8)/9;
    //边长为1的盒子在已经装了的箱子中可以装的数量 
    y=sum*36-a6*36-a5*25-a4*16-a3*9-a2*4;  
    if(y<a1)sum+=(a1-y+35)/36;
    printf("%d",sum);
    return 0;
}