今天是2021年3月13日，mjl 告诉我们，今天要考搜索。

我们：什么玩意儿？？？Σ(っ °Д °;)っ

本人最终成绩：$0+0+70+0+86+10=166$

反正就是挺无语的 qwq。

废话不多说，接下来直接进入

题解时间

T1

某班的学生订了 $N$ 天的午餐，知道他们每天要花多少钱。每天班主任可以选择自己支付或使用班费支付当天午餐费。班主任希望尽可能多地花掉班费，请你帮他计算他最多能够花多少班费。输入包含多个测试数据（不超过 $50$ 个）。$1\leq N\leq 30$，$0\leq M\leq 10^7$。

《论考试不看题不加多组输入考后直接崩掉》

但是其实就是加了估计也要爆零，只是从 WA 变成 TLE 而已。

这就是一道简化版的 The Robbery（考试题目少了一个较为复杂的优化），这里再简单提一下。

基础的搜索很简单，就是在搜索每一天的情况时继续搜索用班费支付和自己支付两种情况。

接下来是剪枝：

首先是排序，按照从大到小排，因为根据简单的贪心思维，先选大的取到最优解的可能性更大。

然后再求一下后缀和，如果在某个情况时前面已经选了的和后面所有没有选的还小于当前最大值，就直接 return。（最优性剪枝）

最后还要注意一下，因为是多组输入，所以统计后缀和的数组需要清空一下。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
int m,n,a[35],ans=0,hzh[35];
bool cmp(int x,int y){
    if(x<y)return false;
    return true;
}
void dfs(int t,int sum){
    if(sum+hzh[t]<ans||sum>m)return;
    if(t==n+1){
        ans=max(ans,sum);
        return;
    }
    //用班费
    if(sum+a[t]<=m)dfs(t+1,sum+a[t]); 
    //不用班费 
    dfs(t+1,sum);
    return;
}
int main(){
    //freopen("lunch.in","r",stdin);
    //freopen("lunch.out","w",stdout);
    while(scanf("%d %d",&n,&m)!=EOF){
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        sort(a+1,a+n+1,cmp);
        for(int i=n;i>=1;i--){
            hzh[i]=hzh[i+1]+a[i];
        }
        dfs(1,0);
        printf("%d\n",ans);
        ans=0;
        memset(hzh,0,sizeof(hzh));
    }
    return 0;
}

T2

有一个 $X\times Y$ 的矩形蛋糕，要分成 $N$ 个面积相同的小块。每一切只能平行于一块蛋糕的一边（任意一边），并且必须把这块蛋糕切成两块。要求 $N$ 块蛋糕的长边与短边的比值的最大值最小。请求出这个比值，输出保留六位小数。$1\le X,Y\le 10000$，$1\le N\le 10$。

这道题主要难在思路（其实也不难），思路出来了基本上就没多大问题了。

这道题目看起来是个二分，但只要稍微冷静地分析一下就会发现这道题不能用二分，再想一下（其实是因为这是一次搜索测试啦），这道题是可以用 DFS 解决的，其思路和巧克力棒差不多。

首先我们假设这是一块长为 $x$ 宽为 $y$ 的蛋糕，需要把它分给 $n$ 个人。

我们可以横着切（平行于 $X$ 轴）或者竖着切（平行于 $Y$ 轴）。那么切哪里呢？

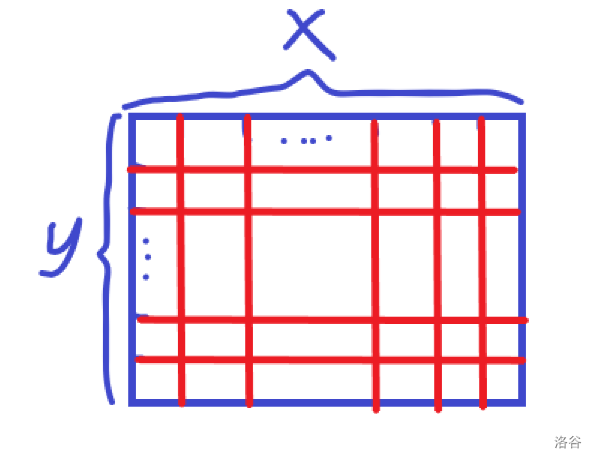
因为我们要把这个蛋糕分给 $n$ 个人，所以我们就切这条边可以被 $n$ 整除的地方。如图。

最后我们来看一下出口：假如说这个 $n=1$ 了，就说明不需要再切了，这个时候我们返回一下长与宽的比值。

（特别注意：最大比例的最小值，不要把 $\max$ 和 $\min$ 用反了）

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
using namespace std;
double bzmax=INT_MAX;
double dfs(double x,double y,int n){
    if(n==1)return max(x,y)*1.0/min(x,y);
    double bzmax=INT_MAX;
    for(int i=1;i<=n/2;i++){//因为切上面和下面都是一样的，所以只用切一半
        bzmax=min(max(dfs(x,i*y/n,i),dfs(x,y-i*y/n,n-i)),bzmax);//x
        bzmax=min(max(dfs(i*x/n,y,i),dfs(x-i*x/n,y,n-i)),bzmax);//y
    }
    return bzmax;
}
int main(){
    //freopen("birthday.in","r",stdin);
    //freopen("birthday.out","w",stdout);
    int x,y,n;
    scanf("%d %d %d",&x,&y,&n);
    printf("%.6lf",dfs(x,y,n));
    return 0;
}

T3

有一个纸片上的数和一个给定的目标数，你需要把纸片切成若干片，要求切出来的每一个数字加起来不超过目标数且与目标数最接近。如果目标数和输入纸片上的数相同，那么纸片不进行切割，如果不论怎样切割，分割得到的纸片上数的和都大于目标数，那么输出错误信息。如果有多种不同的切割方式可以得到相同的最优结果。那么输出拒绝服务信息。你需要给出对纸片的分割方式。输入包括多组数据。
对每一组输入数据，输出相应的输出。有三种不同的输出结果：

  • sum part1 part2 ...（*切割方案）
  • rejected （*拒绝服务）
  • error （*错误信息）

题面很长，但是实质就是添加号问题。

不过添加号真的很难 awa，再加上本人没做对，所以这里就不详细讲了，添加号在我第一周改对了之后直到第二周都还停留在考试的 70 分。

考试 70 分代码（样例倒数第二个有未知玄学错误，大家看看思路就行了）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//*
#include<bits/stdc++.h>
using namespace std;
int s,tot=0,len,ans=0,js=1;
char paper[8];
int a[8],b[8];
void dfs(int t,int sum,int last){//判断t和t+1之间的部分 last：上一个数 
    if(sum+last>s)return;
    if(t==len+1){
        if(sum>ans){
            tot=1,ans=sum;
            int i=1;
            memset(b,0,sizeof(b));
            while(a[i])b[i]=a[i],i++;
        }
        else if(sum==ans)tot++;
        return;
    }
    //切割
    a[js]=last*10+paper[t]-'0';
    js++;
    dfs(t+1,sum+last*10+paper[t]-'0',0);
    a[js]=0;
    js--;
    //不切割 
    dfs(t+1,sum,last*10+paper[t]-'0');
    return;
}
int main(){
    //freopen("paper.in","r",stdin);
    //freopen("paper.out","w",stdout);
    while(1){
        scanf("%d %s",&s,paper+1);
        len=strlen(paper+1);
        if(!s&&paper[1]=='0')return 0;
        dfs(1,0,0);
        if(tot>=2){
            printf("rejected\n");
        }
        else if(tot){
            printf("%d ",ans);
            int i=1;
            while(b[i]){
                printf("%d ",b[i]);
                i++;
            }
            printf("\n");
        }else printf("error\n");
        tot=0,ans=0,js=1;
        memset(a,0,sizeof(a));
    }
    return 0;
}

T4

给出两个单词（开始单词和结束单词）以及一个词典。找出从开始单词转换到结束单词，所需要的最短转换序列。转换的规则如下：

  1. 每次只能改变一个字母。
  2. 转换过程中出现的单词（除开始单词和结束单词）必须存在于词典中，开始单词和结束单词可以不在词典中。如果不能找到这种变换，则输出 0。

《论一个人考试不记得字符串的操作函数然后直接原地爆炸的详细过程》

其实这道题应该不用这些奇奇怪怪的函数也可以做，但是当时看到这道题貌似有点难，想了一会儿思路没出来就去看别的题了。

其实这道题我们可以每一次都统计一下哪些单词和当前的单词可以转换然后在用新的单词继续搜索。

注意一个优化（最优性剪枝），不然会 TLE：

拿一个数组存一下从初始单词到这个单词需要多少步，如果现在我们递归到这个单词时的步数已经大于最优的步数就直接 return。

其实这道题可以用 BFS 做而且据说还好做一点，但是我考试是这么做的就这么写题解吧。

AC 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
int len,n,Min=INT_MAX;
char a[1005][10],end[10];
bool b[1005];
int dp[1005];//记忆化数组，表示从开头到这个单词至少需要几步 
//判断两个单词是否可以互相转换的 check 函数 
bool check(int x,int y){
    int sum=0;
    for(int i=1;i<=len;i++){
        if(a[x][i]!=a[y][i])sum++;
    }
    if(sum==1)return true;
    return false; 
}
// dfs 函数 t：需要操作的字符串 l：目前操作的步数 bh：需要操作字符串的编号 
void dfs(char t[10],int l,int bh){
    //printf("%s %d %d\n",t,l,bh);
    if(l>=Min||dp[bh]&&l>=dp[bh])return;
    dp[bh]=l;
    if(check(bh,n+1)){ // 两个字符串只有一个字符不一样 
        Min=min(Min,l+1);
        return;
    }
    if(l==n)return;
    for(int i=1;i<=n;i++){
        if(!b[i]&&check(bh,i)){
            b[i]=1;
            dfs(a[i]+1,l+1,i);
            b[i]=0;
        }
    }
    return;
}
int main(){
    //freopen("word.in","r",stdin);
    //freopen("word.out","w",stdout);
    scanf("%s %s",a[0]+1,end+1);
    len=strlen(end+1);
    n=1;
    while(scanf("%s",a[n]+1)!=EOF)n++;
    strcpy(a[n+1]+1,end+1);
    dfs(a[0]+1,1,0);
    printf("%d",Min);
    return 0;
}

T5

在一个 $n$ 行 $m$ 列单元格构成的地图中，每一个格子里都有可能是空地（.），墙（#）或者僵尸（G），且四边肯定是墙。若放置一个炸弹，它会以放置点为中心进行行列延伸炸到同行同列的僵尸，但不能穿墙。
有一个人去放一个炸弹，他初始位置在 $(x,y)$，只能在地图中朝上下左右四个方向行进，不能穿墙，也不能穿越僵尸。求最多能炸到的僵尸数量。

考场上打了个广搜+记忆化得了 $80$ 分，后来讲题的时候 mjl 说：

在两堵墙之间，横向或纵向能炸到僵尸的数量相同。

然后我就很 zz 的在函数里面加上了这个优化……

最终从 80 掉到了 75。

后来我去问 mjl，他给我看了个 AC 代码……（这玩意儿还是要加在主函数里的？！）

AC 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
char a[2005][2005];
bool b[2005][2005];
int dp1[2005][2005],dp2[2005][2005],dp3[2005][2005],dp4[2005][2005];
int m,n,x,y,ans=-1;
int dir[4][2]={{-1,0},{0,-1},{1,0},{0,1}};
struct s{
    int x,y;
}t1,t2;
void bfs(int x,int y){
    queue<s> q;
    t1.x=x,t1.y=y;
    q.push(t1);
    int dx,dy;
    while(!q.empty()){
        t1=q.front();
        q.pop();
        for(int i=0;i<=3;i++){
            dx=t1.x+dir[i][0],dy=t1.y+dir[i][1];
            if(dx>=1&&dx<=m&&dy>=1&&dy<=n&&!b[dx][dy]&&a[dx][dy]!='#'&&a[dx][dy]!='G'){
                b[dx][dy]=1;
                if(dp1[dx][dy]+dp2[dx][dy]+dp3[dx][dy]+dp4[dx][dy]>ans)
                    ans=dp1[dx][dy]+dp2[dx][dy]+dp3[dx][dy]+dp4[dx][dy];
                t2.x=dx,t2.y=dy;
                q.push(t2);
            }
        }
    }
    return;
}
int main(){
    //freopen("zombie.in","r",stdin);
    //freopen("zombie.out","w",stdout);
    scanf("%d %d %d %d",&m,&n,&x,&y);
    for(int i=1;i<=m;i++){
        scanf("\n");
        for(int j=1;j<=n;j++){
            scanf("%c",&a[i][j]);
            if(a[i][j]=='G'){
                dp1[i][j]=dp1[i][j-1]+1;
                dp2[i][j]=dp2[i-1][j]+1;
            }else{
                dp1[i][j]=dp1[i][j-1];
                dp2[i][j]=dp2[i-1][j];
            }
            if(a[i][j]=='#'){
                dp1[i][j]=0;
                dp2[i][j]=0;
            }
        }
    }
    for(int i=m;i>=1;i--){
        for(int j=n;j>=1;j--){
            if(a[i][j]=='G'){
                dp3[i][j]=dp3[i][j+1]+1;
                dp4[i][j]=dp4[i+1][j]+1;
            }else{
                dp3[i][j]=dp3[i][j+1];
                dp4[i][j]=dp4[i+1][j];
            }
            if(a[i][j]=='#'){
                dp3[i][j]=0;
                dp4[i][j]=0;
            }
        }
    }
    bfs(x,y);
    printf("%d",ans);
    return 0;
}

T6

一个人进入了一个两层的迷宫，迷宫的入口是 $S(0,0,0)$，里面有时空传输机（用 # 表示），墙（用 * 表示），平地（用 . 表示）。进入时空传输机会被转到另一层的相对位置，但如果被转到的位置是墙，他就会被撞死。他只能在一层中前后左右移动，每移动一格花 $1$ 时刻。层间的移动只能通过时空传输机，且不需要任何时间。如果他能在 $T$ 时刻及以前到 $P$ 点输出 YES，否则输出 NO。多组数据。 $1 <= N,M <=10$。

其实我根本不知道自己考试的代码为什么会错，但是经过了代码的重构与 mjl 的帮助之后我 A 了这道题。

首先思路 BFS，其他的内容和走迷宫的 BFS 经典题目差不多，唯一的区别就是传送门，如果走到了传送门就传送到另外一层，并且这两个传送门都会走一遍。需要特别注意的是不要陷入上下两个都是传送门的死循环。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include<bits/stdc++.h>
using namespace std;
int m,n,T;
char a[15][15][2];
bool b[15][15][2];
int dir[4][2]={{-1,0},{0,-1},{1,0},{0,1}};
struct s{
    int x,y,z,l;
}t1,t2;
//取相反数：0到1，1到0 
int f(int x){
    if(x)return 0;
    return 1;
}
bool bfs(int x,int y,int z){
    queue<s> q;
    t1.x=x,t1.y=y,t1.z=z,t1.l=0;
    q.push(t1);
    int dx,dy;
    while(!q.empty()){
        t1=q.front();
        q.pop();
        //特判：#和P
        if(a[t1.x][t1.y][t1.z]=='#'){
            if(a[t1.x][t1.y][f(t1.z)]=='P'||a[t1.x][t1.y][f(t1.z)]=='.'){
                t1.z=f(t1.z);
                q.push(t1);
            }
            continue;
        }else if(a[t1.x][t1.y][t1.z]=='P')return true;
        for(int i=0;i<=3;i++){
            dx=t1.x+dir[i][0],dy=t1.y+dir[i][1];
            if(dx>=1&&dx<=m&&dy>=1&&dy<=n&&a[dx][dy][t1.z]!='*'&&!b[dx][dy][t1.z]){
                b[dx][dy][t1.z]=1;
                t2.x=dx,t2.y=dy,t2.z=t1.z,t2.l=t1.l+1;
                if(t2.l>T)continue;
                q.push(t2);
            }
        }
    }
    return false;
}
int main(){
    freopen("plan.in","r",stdin);
    freopen("plan.out","w",stdout);
    int c,x,y,z;
    scanf("%d",&c);
    while(c--){
        memset(b,0,sizeof(b));
        scanf("%d %d %d",&m,&n,&T);
        for(int i=1;i<=m;i++){
            scanf("\n");
            for(int j=1;j<=n;j++){
                scanf("%c",&a[i][j][0]);
                if(a[i][j][0]=='S')x=i,y=j,z=0;
            }
        }
        scanf("\n");
        for(int i=1;i<=m;i++){
            scanf("\n");
            for(int j=1;j<=n;j++){
                scanf("%c",&a[i][j][1]);
                if(a[i][j][1]=='S')x=i,y=j,z=1;
            }
        }
        if(bfs(x,y,z))printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

总结时间

T1 没看到多组输入，以为就是道水题，看到题目的背景之后没有任何联想，也没有想到那道让我犹豫了很久的 The Robbery，导致一道本来会做的题丢掉 $100$ 分。

T2 本来这么水一道题也没有想到思路，这道题应该就是那种思路很难想，但是一想出来就很简单的那种题吧，得亏我们之前还做过一道类似的题目……

T3 出了一个 bug，然后我在那个地方调了很久，其实当时应该先把这个部分分拿到之后就先去看别的题目，因为 bug 不好说什么时候调得出来，可是有些题的部分分是很好得的……

T4 因为不会函数就直接跳过了，其实就相当于我又跳过了一道比较简单的题目，所以事实证明：

  1. 函数不会不要虚，有时候手打函数比系统自带的还要快，比如说$\max$，$\min$ 等。
  2. 要背常用函数。

T5 的话，还是优化方法没有完全掌握吧……平时刷题不够多。

T6 属于那种过完样例就走人行为，因为 $10$ 分的话确实太少了……

所以经过这次考试，可以发现：

  • 考试比赛如果题目比较难，骗分和部分分永远是王道（*＾-＾*）。
  • 常用函数是一定要背的（而且不要被错），考试用节约时间，但是如果背不到也不要直接放弃题目，只要你手打得出来就继续做。（当然如果这道题做不出来就另当别论了！）
  • 安排好考试时间，如果一道题有 bug，不管可不可以拿到一部分分，也先不要在这道题死磕（尤其是死磕超过一节课的时间），先去看一下别的题有没有思路了。
  • 认真读题。尤其注意别漏了恶心人的多组输入。
  • 要充分发挥自己的联想能力。要定期复习代码，不要以为 AC 了就万事大吉，这样考试的联想才能发挥作用。

希望这篇博客可以帮助到大家（还有我自己），感谢观看！