前置芝士

  • 二分的递归写法
  • 二叉树

线段树

线段树（Segment Tree）是一种二叉树，本质上和树状数组有区别虽然都是树。

不过和树状数组一样，线段树也是一种维护数组的数据结构，它可以实现 $O(\log n)$ 修改、查询不过常数比树状数组大得多。

另外，线段树的应用范围比树状数组广，不过它维护的数据必须满足结合律（$eg.(a+b)+c=a+(b+c)$）。为什么呢？这涉及到线段树实现的原理。

性质 & 原理

首先要建一棵线段树，首先我们要有一个线段，那就是数组。

然后，我们还需要一棵二叉树。

于是，我们就成功种了一棵线段树。

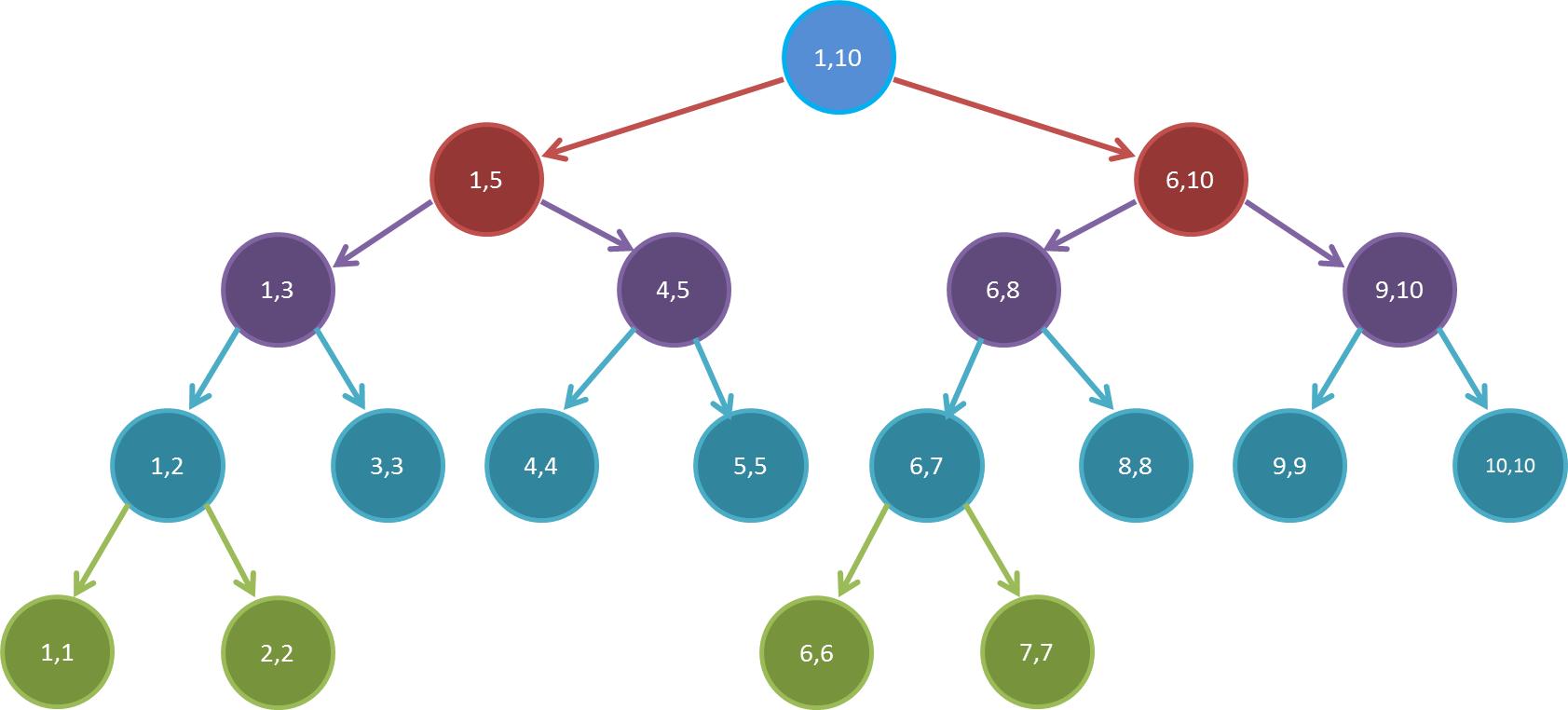
它长这样：

注意到每个结点里面的区间没，这是闭区间，代表的是这个结点存的信息来源于数组的哪个区间。

观察这个线段树，我们可以发现：

  • 每个叶子结点都代表数组中的一个元素。

  • 每个非叶子结点的两个孩子的区间是从父节点区间的中间划开的。

    说详细一点，若一个非叶子结点覆盖的区间为 $[L,R]$，那么令 $mid=\lfloor \frac{L-R}{2}\rfloor$，则左孩子覆盖的区间为 $[L,mid]$，右孩子覆盖的区间为 $[mid+1,R]$。

  • 除去最后一行是一棵满二叉树。

那线段树的原理是怎样的呢？这里我们先讲最简单的单点修改、区间查询来理解。

有点类似于于归并排序，我们需要分解后再合并数据。每个父节点存储的信息都是其两个子节点信息的合并，这样我们就可以通过访问一个结点拿到这个节点所代表区间的信息。

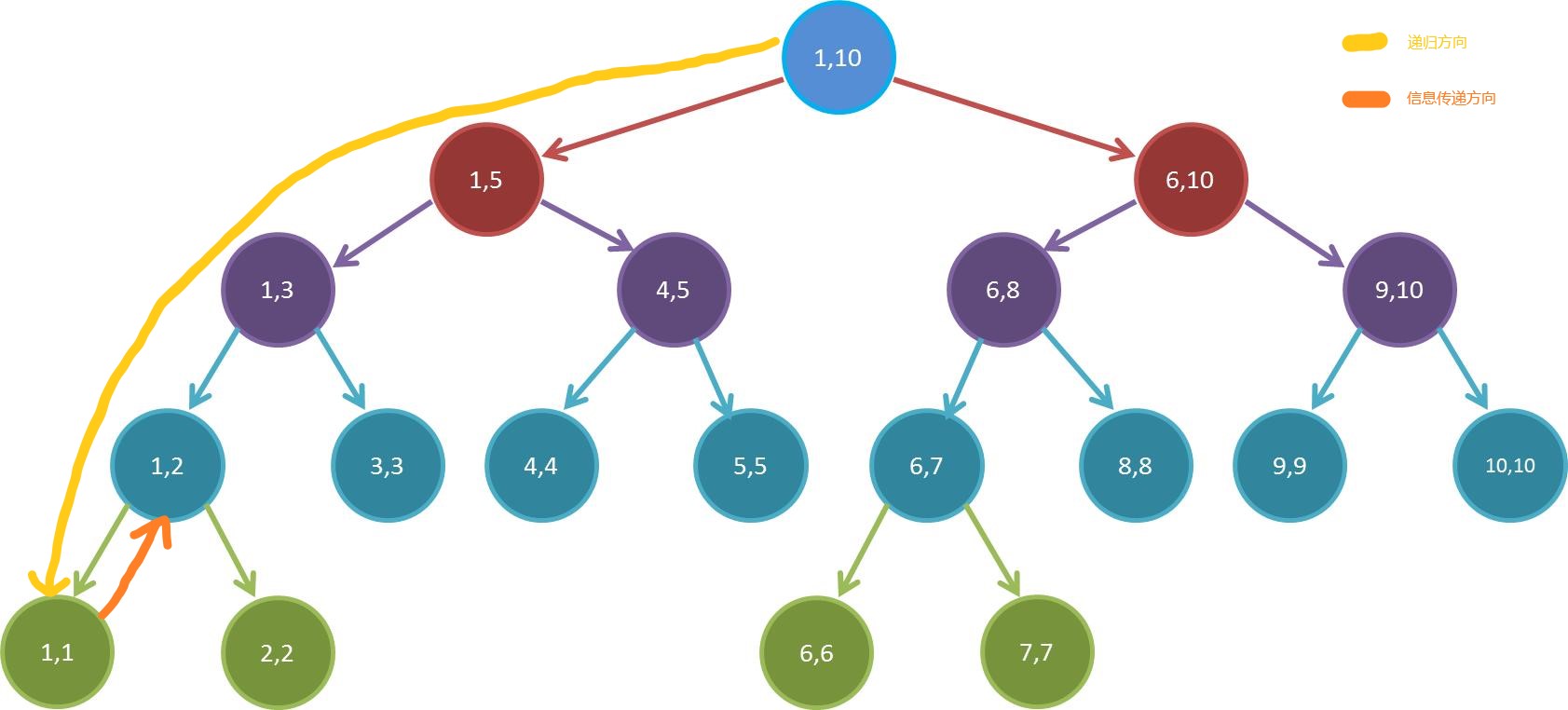
首先分解，我们一层一层往下递归，直到找到叶子结点，然后把叶子结点的信息向它的父节点传递：

向上传递信息

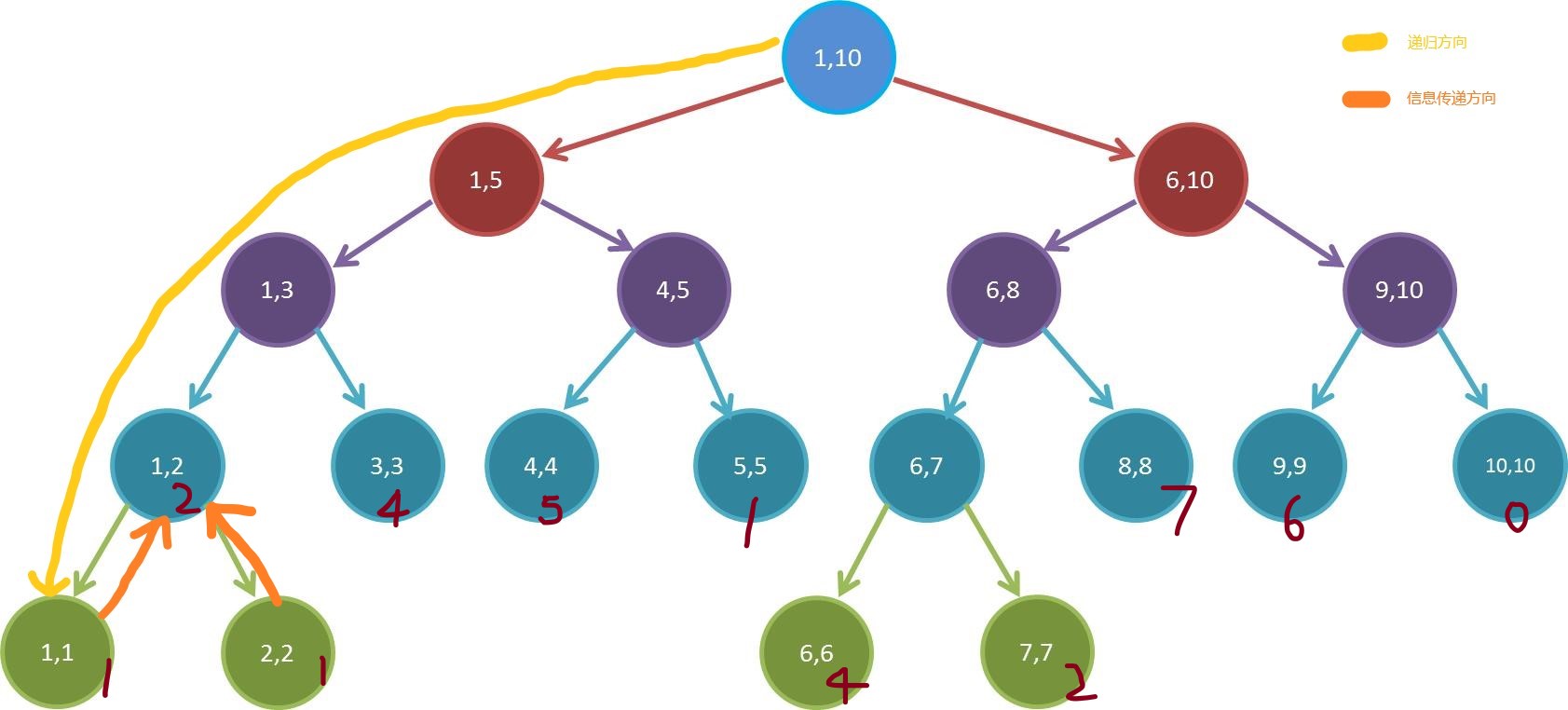
然后由于递归回溯的原因，我们会接着遍历到它的兄弟，这个时候，它的父节点已经获得了两个子节点的信息，就可以合并信息了。

这个地方，我们给数组一个值，然后用数组元素和来代表需要求解的信息。

赋值

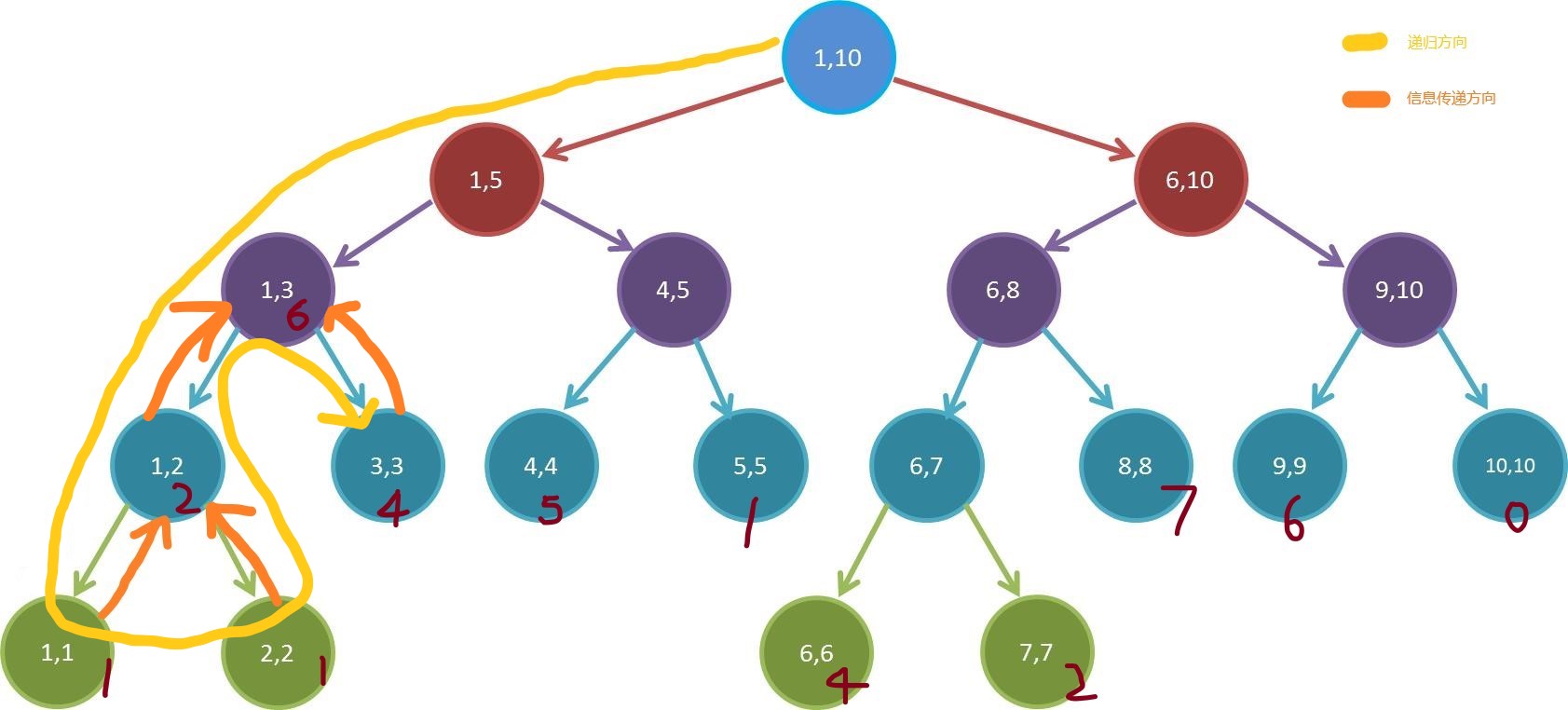
我们继续往上回溯，按照相同的方法求解。在求解 $[1,3]$ 之前，我们需要把 $[1,2]$ 的值先传上去。

再往上

这么一点一点的传上去，就可以求得区间的和了！

这个操作的时间复杂度是 $O(\log n)$，每次修改、查询和初始化的时候都这么来一遍，不就可以实现单点修改区间查询了嘛。

那么为什么求得的值必须满足结合律呢？显而易见，我们需要把求解的值分成一个区域一个区域地求解，如果不满足结合律就会出问题。

接下来我们来讲一讲 C++ 的实现。

存储

于是我们知道，每一个结点里需要存：

  • 区间左端点 $l$
  • 区间右端点 $r$
  • 这个区间的信息（$eg.\sum_{i=l}^{r}a_i$ 或者 $\max^{r}_{i=l}{a_i}$）

等等，为什么不用存左孩子和右孩子呢？

这就涉及到存储线段树的方法。

一般来说，只要题目不卡空间，我们可以通过数组来存一个本质上是二叉树的线段树：

根节点数组下标是 $1$，对于每个非叶子节点，若它的数组下标是 $p$，那么其左孩子数组下标是 $2p$，右孩子数组下标是 $2p+1$。

那么，处理好存储的问题，接下来我们来解决初始化。

初始化 & 单点修改

对于一段区间 $[l,r]$，我们把它从 $mid$ 分成 $[l,mid]$ 和 $[mid+1,r]$，然后以这两个区间作为此结点的两个子节点。

像开头说的那样，我们一直往下递归，当递归到叶子结点的时候就把数组的值赋给叶子结点，接着我们把叶子结点的信息传到它的父结点，然后求父结点的值，再把父结点的信息传给父结点的父结点……最终就可以把信息传递到根节点了。

请注意，儿子向父亲转移需要放在递归语句的后面。除此之外没有什么别的难点，看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 这两行代码是求左子树和右子树下标的函数，p << 1 等价于 p * 2，p << 1 | 1 等价于 p * 2 + 1，不过速度更快
inline int lc(int p) { return p << 1; }
inline int rc(int p) { return p << 1 | 1; }

void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r; // 给结点代表的区间端点赋值
    if(l == r) { // 这个节点是叶子节点，没有子树
        t[p].val = a[l]; // 赋值
        return;
    }
    int mid = (l + r) >> 1;
    build(lc(p), l, mid);     // 初始化左子树
    build(rc(p), mid + 1, r); // 初始化右子树
    t[p].val = t[lc(p)].val + t[rc(p)].val; // 合并左右子树的信息
    return;
}

单点修改的代码和初始化很像，不过还是有一点区别。

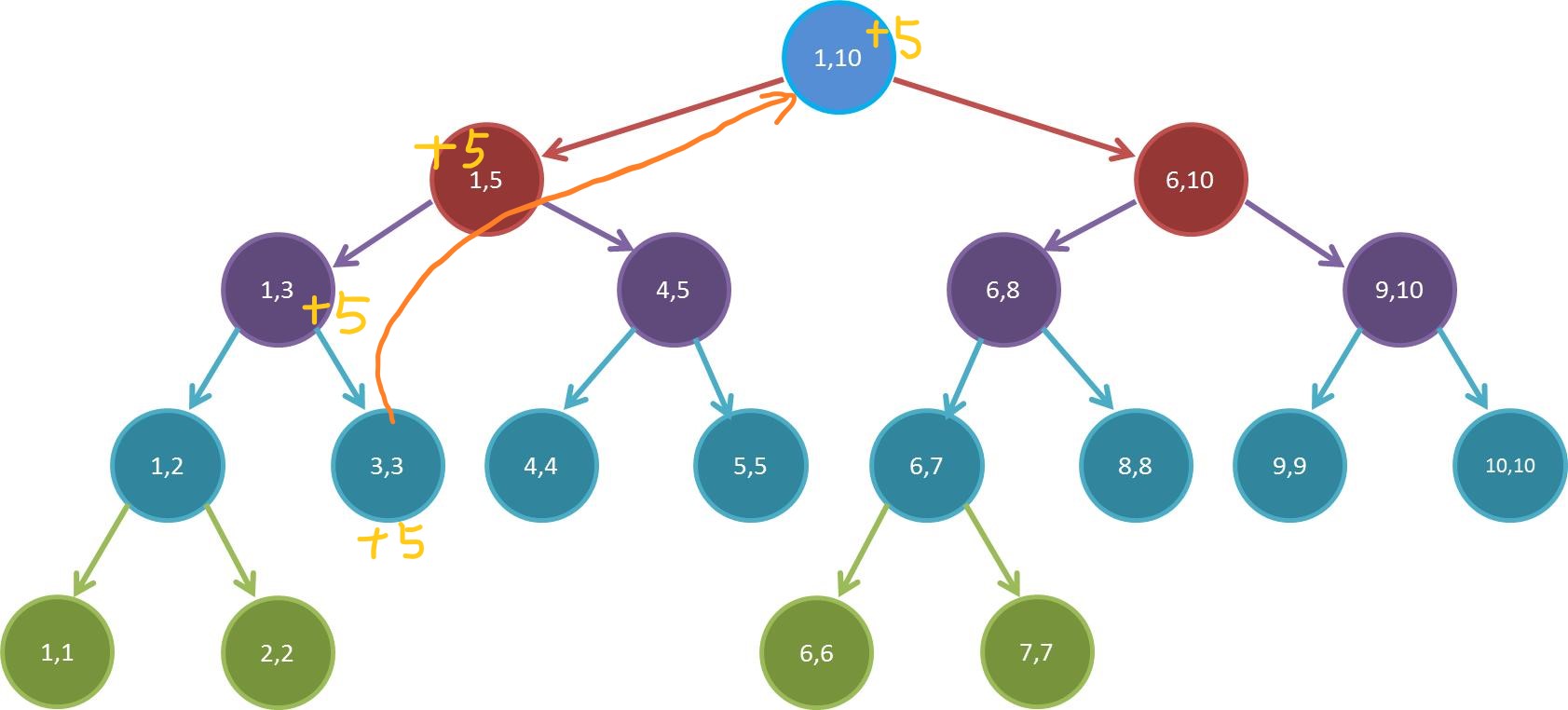
假设我们要修改下标为 $3$ 的数字，把它加上 $5$：

就像这样，我们要在每一个包含所修改数据的下标的区间加上 $5$。

那么整个 $\text{update}$ 函数有这两个部分：

  1. 从根节点出发往下找，直到找到需要修改的点（叶子节点）；

  2. 往上回溯过程中修改每一个经过的结点的值。

那么代码就呼之欲出了：

1
2
3
4
5
6
7
8
9
10
11
12
13
void update(int p, int x, int k) {
    if(t[p].l == t[p].r) { // 找到了需要修改的叶子节点
        t[p].val = k; // 修改它的值
        return;
    }
    int mid = (t[p].l + t[p].r) >> 1;
    if(mid >= x) // 如果需要修改的结点在左子树
        update(lc(p), x, k);
    else // 需要修改的结点在右子树
        update(rc(p), x, k);
    t[p].val = t[lc(p)].val + t[rc(p)].val; // 合并左右子树的信息
    return;
}

区间查询

我们可以找一些结点，且这些结点的范围能够刚好覆盖需要查询的区间，把这些结点的权值合并就可以了。

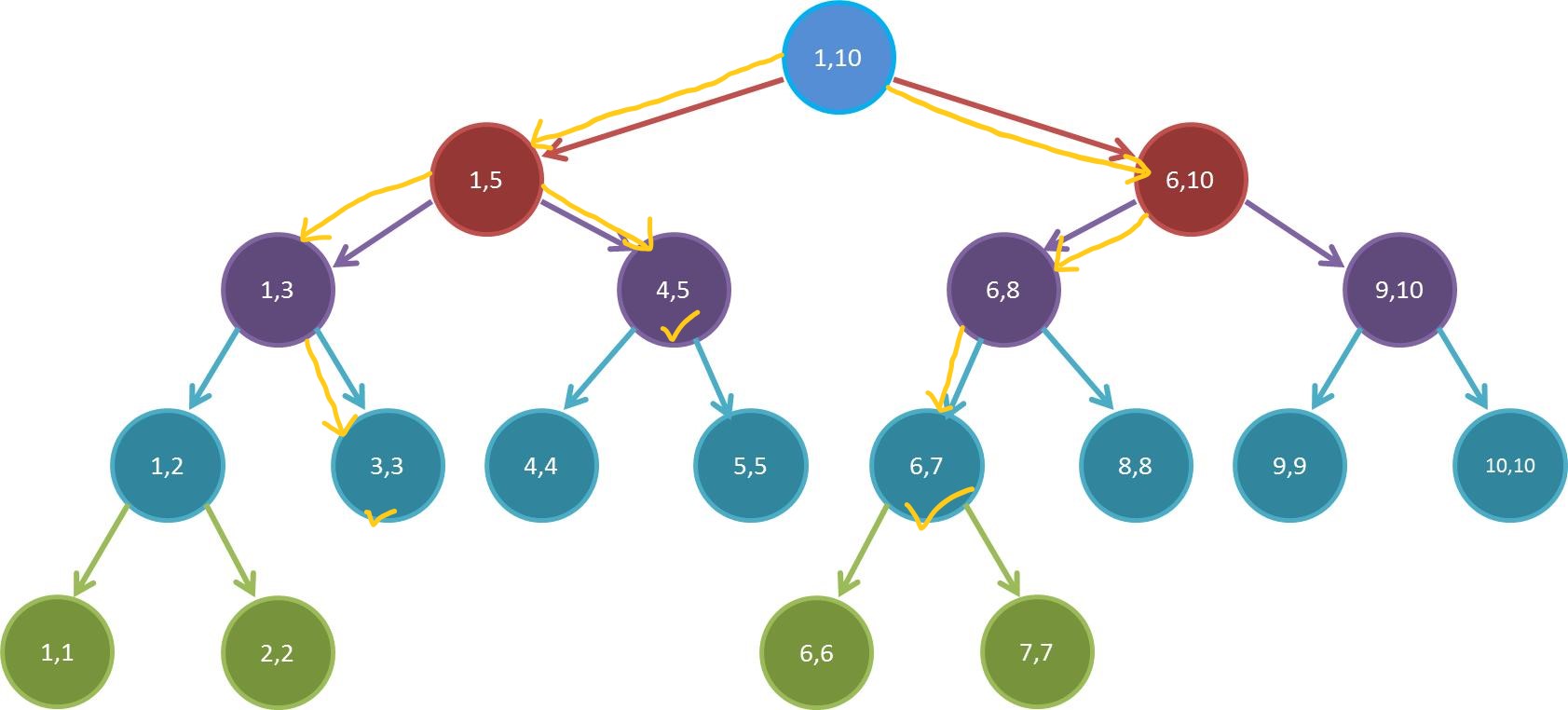
那怎么找呢？我们来看一张图：

这张图是我们在查询区间 $[3,7]$ 时的过程。

在递归的时候，有以下几条准则：

  1. 如果当前区间能完全被待查区间包含，就返回此区间的权值并不再往下递归。（图中打勾的地方）
  2. 如果当前区间被待查区间部分包含，就继续往下递归。
  3. 如果发现当前区间完全不能被当前区间包含，就停止递归。

当然，这里还有个难点，就是怎么判断是否应该递归到某个结点的左子树或者右子树呢？

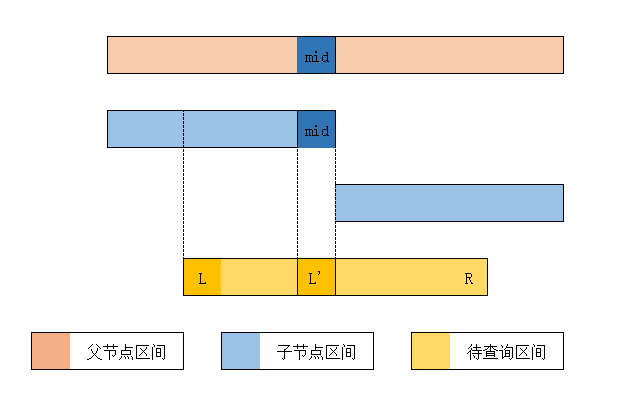
我们都知道，线段树中两个子节点的区间是从父节点区间的中间切开的。所以，如果要判断左子树是否需要递归，就应该这样：

假设待查询区间是 $[L,R]$，我们会发现，只有在 $L\le mid$ 时，左区间才会被（至少是部分）包含。

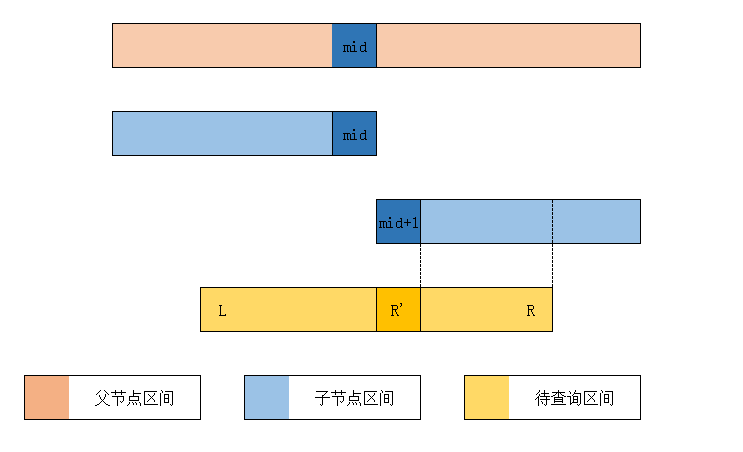
右区间同理：

需要满足的条件是 $R\ge mid+1$，也就是 $R>mid$。

代码长这样：

1
2
3
4
5
6
7
8
9
10
11
int query(int p, int l, int r) {
    int sum = 0;
    if(l <= t[p].l && t[p].r <= r)
        return t[p].val;
    int mid = (t[p].l + t[p].r) >> 1;
    if(l <= mid)
        sum += query(lc(p), l, r);
    if(r > mid)
        sum += query(rc(p), l, r);
    return sum;
}

区间修改

众所周知单点修改线段树的时间复杂度是 $O(\log n)$，那么如果是区间修改，如何保持时间复杂度不变呢？

你可能会回答：差分。是的，这是一个可行的方法，不过差分只能维护区间和的查询，而对于查询最大值等则束手无策。而且既然如此，直接打码量少常数小的树状数组他不香吗。

于是一个玄学的方法出现了：懒惰标记。

我们知道，对于一个区间的修改，后面的查询不一定用得到，比如有一次你修改区间 $[1,5]$ 但是后面根本没有查询这里的值，那么我们就没有必要在修改的时候把所有的子节点都修改一遍，只有需要的时候才修改。

懒惰标记就是这么一个东西，我们给一个节点打上懒惰标记，就意味着这个结点的值已经被修改过，但是它的子节点还没有被更新。 只有我们在后面操作中需要更新后面的值，才需要把懒惰标记传到下面，更新需要的值。

在区间修改的时候，如果我们递归到一个结点覆盖的区间被需要修改的区间完全包含，那么我们就不需要再递归下去，而是给这个结点更新后打上一个懒惰标记，意味着这一段区间需要被修改，但是还没有完全实际操作。等下一次我们需要查询用到里面的值时，递归到这个节点时，我们就知道下面还没有更新，所以就把这个节点的两个子节点更新，然后把懒惰标记传到子节点上，以此类推。

把懒惰标记从父节点传到子节点的过程我们可以用一个 $\text{pushdown}$ 函数实现。在这个函数里面，我们先需要修改子节点的权值，然后把父节点的懒惰标记叠加到子节点的懒惰标记上，最后清空父节点的懒惰标记，代码如下：

1
2
3
4
5
6
7
8
9
10
// target 即为懒惰标记
inline void down(int p) {
    int l = lc(p), r = rc(p);
    t[l].val += (t[l].r - t[l].l + 1) * t[p].target;
    t[r].val += (t[r].r - t[r].l + 1) * t[p].target;
    t[l].target += t[p].target;
    t[r].target += t[p].target;
    t[p].target = 0;
    return;
}

一些扩展

线段树不仅可以维护诸如区间和，最值之类，还可以维护一些奇奇怪怪的东西。

先来看第一组：

GSS1 GSS3

要求的是一个区间的最大子段和。

想一下，把两个区间合并为一个区间，该怎么找到这个区间的最大子段和呢？

无非就三种情况嘛：

  1. 左边的最大子段和；
  2. 右边的最大子段和；
  3. 左边包含右端点的最大子段和加上右边包含左端点的最大子段和。

那这三个东西怎么求呢？