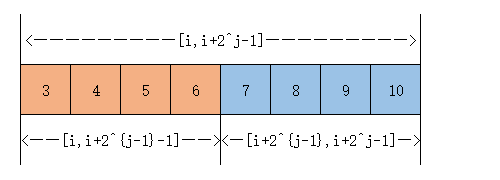1. RMQ 是啥

RMQ (Range Minimum / Maximum Query）问题是指：对于长度为 $n$ 的数列 $A$，回答若干询问 $\text{RMQ}(A,i,j)(1\leq i,j\leq n)$，返回数列 $A$ 中下标在 $[i,j]$ 里的最小（大）值，也就是说，RMQ 问题是指求区间最值的问题。

全是抄的。

也就是说，RMQ 是一类问题，而不是一类数据结构。

所以暴力（没有初始化，查询$\Theta(n)$），线段树（初始化和查询都是 $\Theta(\log n)$）等都可以解决 RMQ 问题。

那么是否有更♂快的方法呢？

有！就是 ST 表。

2. 概念

ST 表通过 DP 的方式，可以实现 $\Theta(n\log n)$ 初始化，$\Theta(1)$ 查询区间最值。

优点：最重要的，快！

缺点：不支持修改数组，而且空间复杂度为 $\Theta(n\log n)$，可能会受不了。

3. 实现

$dp_{i,j}$ 代表从 $i$ 开始，区间长度为 $2^j$ 的区间，即 $[i,i+2^j)$ 的最值（可以是最大值或者最小值，这个无所谓）。

初始化

对于 $\forall i,j=0$ 时，区间只有 $A_i$ 这一个数字，所以肯定最值是 $A_i$。

状态转移

我们知道，对于任意一个长度为 $2$ 的幂次方的区间，都可以划分为长度相等的两部分，例如 $[3,10]$ 就像这样：

（$i=3,j=3$）

也可以说明区间 $[i,i+2^j)$ 可以被分为 $[i,i+2^{j-1})$ 和 $[i+2^{j-1},i+2^j)$ 两个部分，每个部分的长度都是 $2^{j-1}$。

那么转移方程不就出来了吗：

当然，在代码的实现过程中，我们可以用 1 << x 来代替分析中的 $2^x$，不过需要注意的是，位运算的优先级比四则运算低，需要打括号。

查询

对于任意一个区间 $[i,j]$，如何用已经初始化好的 ST 表求解最值呢？

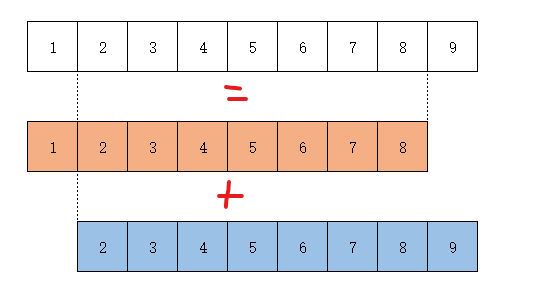
看图：

我们可以把任意一个区间分解成这样两个长度为 $2$ 的幂次的区间，一个区间左端点为待求区间的左端点，另一个区间的右端点为待求区间的右端点，两个区间的长度为所有 $2$ 的幂次中小于 $j-i+1$ 的最大的那一个，转换一下就变成了可以用 $2$ 的幂次表示的 $2^{\lfloor\log_2(j-i+1)\rfloor}$。（PS：$2^{\log_2(x)}=x$）。

找到两个分解后的区间，求一下最值就行了。

数列区间最大值问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <cstdio>
#include <cmath>
#define rep(i, j, k) for(int i = j; i <= k; ++i)
#define dep(i, j, k) for(int i = j; i >= k; --i)

const int maxn = (int)1e5 + 5;

int n, q, a[maxn], dp[maxn][1005];

inline int max(int x, int y) { return x > y ? x : y; }

inline void init() {
    rep(i, 1, n)
        dp[i][0] = a[i];
    for(int j = 1; 1 << j <= n; ++j)
        for(int i = 1; i + (1 << j - 1) - 1 <= n; ++i)
            dp[i][j] = max(dp[i][j - 1], dp[i + (1 << j - 1)][j - 1]);
    return;
}

inline int rmq(int l, int r) {
    int k = log2(r - l + 1); // cmath 库中有内置的 log2 函数，请注意不要用成以 e 为底的 log 函数
    return max(dp[l][k], dp[r - (1 << k) + 1][k]);
}

int main() {
    scanf("%d %d", &n, &q);
    rep(i, 1, n)
        scanf("%d", &a[i]);
    init();
    int l, r;
    rep(i, 1, q) {
        scanf("%d %d", &l, &r);
        printf("%d\n", rmq(l, r));
    }
    return 0;
}

4. 应用

ST 表本身就是个工具，我们在平时做题的时候不能想着刻意去使用它，详情参考洛谷 P2048 。

另外，ST 表之所以有局限性，是因为它在查询的时候可能会有一部分区间被重复查询，所以只能求解那些有重复元素不影响最终结果的问题。这种问题除了最大最小值之外，还有 gcd、lcm 等，所以这些问题也是可以通过 ST 表求的。