单调队列优化

大家是不是经常看到一道 DP 题的状态转移方程长这样：

这个状态转移方程需要满足三点：

  1. $L$ 随着 $i$ 的增大而不下降，也就是说把 $i$ 从 $1$ 到 $n$ 时的 $L$ 按照 $i$ 升序排序，这个序列是不严格递增的；
  2. $h(j)$ 是一个在所有变量中（比如 $i,j$ 等）只与最内层循环变量的式子；
  3. $g(i)$ 是一个在所有变量中只与不是最内层循环变量有关的式子。

举个栗子，这个状态转移方程就是合法的（假设除了 $i,j$ 之外所有值都是已知的）：

$dp_i=\max\limits_{j=i-m}^{i-1}\{dp_j+num_i\}$

（您可以把 $+num_i$ 挪到 $\max$ 的外面去，这样可以看得更清楚。）

但是这个状态转移方程就是不合法的，因为 $h(j)$ 与 $j,k$ 都有关：

$dp_{i,j}=\max\limits_{k=i-m}^{i-1}\{dp_{i,j-k+1}+num_i\}$

这个状态转移方程也不是合法的，因为 $g(i)$ 与 $j$ 也有关系：

$dp_i=\max\limits_{j=i-m}^{i-1}\{dp_j+num_j\}$

那我们该如何利用这三个特性呢？

答案是，单调队列！

假设要求求最大值，我们就用一个单调递增队列来维护在外层循环变量不相同的情况下，那个只与最内层循环变量有关的函数 $\bf{h}$ 的值。拿上面举例子的第一个状态转移方程来说，遍历到每一个 $i$ 时，需要做的事情如下：

  1. 排除单调队列头已经“过期”的值。$j<i-m$ 的值不会再用到了，为了避免重复算到，需要直接弹出去。
  2. 此时单调队列头的那个元素就是我们能找到的最优的 $j$，用这个 $j$ 进行状态转移（所以要在单调队列里面存下标，即 $j$，但是排序是按照 $h(j)$ 排的）。
  3. $i$ 从队列尾入队。当然因为是单调队列，所以进去之前先把不符合要求的从队尾弹出来。

过程很好理解。但是如何证明每次那个左端的值就是最优的 $j$ 呢？

这也就涉及到需要满足的那三个条件。一条一条看：

  1. 第一条保证了在弹出“过期”元素的过程中不会误把需要的元素弹出去。
  2. 第二条，由于 $h(j)$ 只与 $j$ 有关，所以只要 $j$ 确定了，$h(j)$ 的值也就确定了，单调队列的单调性就得到了保证，这样才能证明队列左端的 $\bf{j}$ 是最优的。
  3. 第三条，$g(i)$ 与 $j$ 无关，那么状态转移方程的外部就不会受到 $j$ 的影响，这样才能保证在 $j$ 最优的情况下，状态转移方程得到的值最优。

注意：$j$ 最优和状态转移方程得到的值最优是两回事，因为我们考虑 $j$ 最优只考虑了 $h(j)$ 而非整个状态转移方程。

单调队列优化可以直接把最里面一层循环 pass 掉，经过优化后复杂度降次，$\Theta(n^2)$ 可直接变为 $\Theta(n)$。

理论可行，实践开始。

例题一

「USACO11OPEN」Mowing the Lawn G

这道题的三种 DP 方法都不难，我想出来的是逆推的方法：

$dp_i$ 代表第 $i$ 头奶牛不干活且满足条件时最小的效率损失。状态转移方程如下：

最终答案 $ans=\sum\limits_{i=1}^n E_i - dp_{n+1}$。

用一个单调递减队列维护 $dp_j$，按照上述方法一步一步操作即可。

注意：打单调队列优化时一定一定要注意 q[L] / q[R] 与 dp[q[L]] / dp[q[R]] 的区别！（我已经因为这个挂了两次了 qwq）

对于这道题，还有两个注意点：

  1. 要开 long long；
  2. 由于最后一头奶牛不一定不干活，$dp_{n+1}$ 才是最终的答案。

非常简洁的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <cstdio>
#define ll long long
#define rep(i, j, k) for(int i = j; i <= k; ++i)
#define dep(i, j, k) for(int i = j; i >= k; --i)

const int maxn = (int)1e5 + 5;

int n, k, e[maxn];
int L, R, q[maxn];
ll s, dp[maxn];

int main() {
    scanf("%d %d", &n, &k);
    rep(i, 1, n) {
        scanf("%d", &e[i]);
        s += e[i];
    }
    rep(i, 1, n + 1) {
        while(L < R && q[L] < i - k - 1) // Step 1
            ++L;
        dp[i] = dp[q[L]] + e[i]; // Step 2
        while(L < R && dp[q[R]] > dp[i]) // Step 3(1)
            --R;
        q[++R] = i; // Step 3(2)
    }
    printf("%lld", s - dp[n + 1]);
    return 0;
}

例题二

「一本通 5.5 练习 1」烽火传递

状态转移方程：

注意需不需要 $-1$ 的判断：其实就判断连续 $m$ 个东西状态都为好的那种状态是不是可行的，如果可行就 $-1$，如果不可行就不减。比如例题一，连续 $k$ 头奶牛干活是可行的，只有超过 $k$ 头才会出问题，所以可以 $-1$；这道题连续 $m$ 个烽火台不放火是不可行的，所以不减。

我可真是个水文小能手 hhh。

把上面的代码改改就过了。

例题三

「一本通 5.5 练习 2」绿色通道

这题目一看就是二分，$\text{check}(l)$ 用 DP 计算最多连续空 $l$ 道题时最小的时间，再看一下这个时间和给出时间的大小关系来判断 $l$ 是否满足条件。

状态转移方程（和前面差不多就不讲了）：$dp_i=\min\limits_{j=i-m}^{i-1}\{dp_j\}+a_i$

初始化一定要初始化干净。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <cstdio>
#define rep(i, j, k) for(int i = j; i <= k; ++i)
#define dep(i, j, k) for(int i = j; i >= k; --i)

const int maxn = (int)5e4 + 5;

int n, t, a[maxn], dp[maxn];
int L, R, q[maxn];

inline void init() {
    L = R = 0;
    rep(i, 1, n)
        q[i] = dp[i] = 0;
    dp[n + 1] = 0;
    return;
}

inline bool check(int l) {
    init();
    rep(i, 1, n + 1) {
        while(L < R && q[L] < i - l - 1)
            ++L;
        dp[i] = dp[q[L]] + a[i];
        while(L < R && dp[q[R]] > dp[i])
            --R;
        q[++R] = i;
    }
    return dp[n + 1] <= t;
}

int f(int l, int r) {
    if(l == r)
        return l;
    int mid = (l + r) >> 1;
    if(check(mid))
        return f(l, mid);
    return f(mid + 1, r);
}

int main() {
    scanf("%d %d", &n, &t);
    rep(i, 1, n)
        scanf("%d", &a[i]);
    printf("%d", f(0, n));
    return 0;
}

斜率优化

上面我们讲了单调队列优化可以很明显地优化时间复杂度，但是要用它限制较多。如果说自变量和 $i$ 和 $j$ 都有关系该怎么办呢？

引入

关于一次函数

在平面直角坐标系中，一次函数的一般式形为：$y=kx+b$。

两点确定一条直线，如果知道 $y$ 上两点的坐标 $(x1,y1),(x2,y2)$，那就可以确定 $y$。其中 $k$ 的求法为：

最小截距

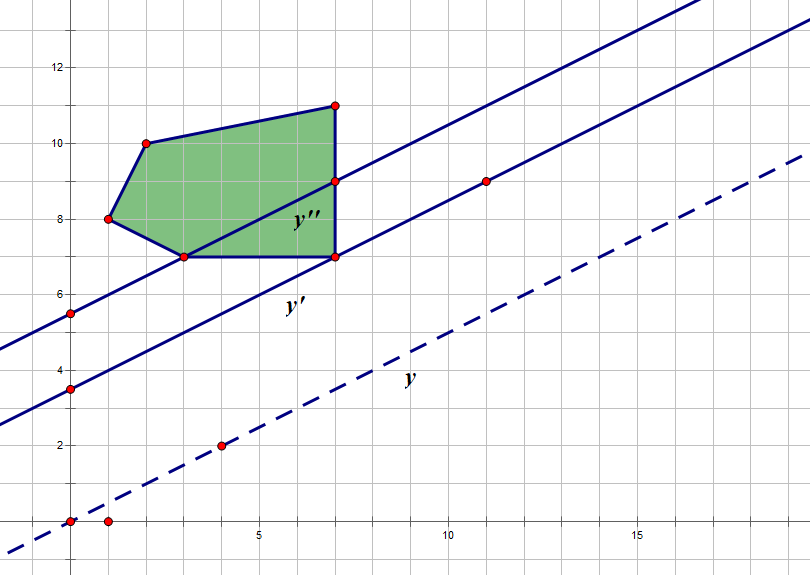
$y=kx(k>0)$ 为一次函数，有个多边形在此函数上方，平移 $y$ 得到 $y’=kx+b$，使得 $y’$ 穿过多边形（穿过顶点也算）且 $b$ 最小，该怎么平移呢？

把 $y$ 向上平移，直到多边形的一个顶点第一次到了直线上，就找到了最优解。如图，$y’$ 优于 $y’’$。

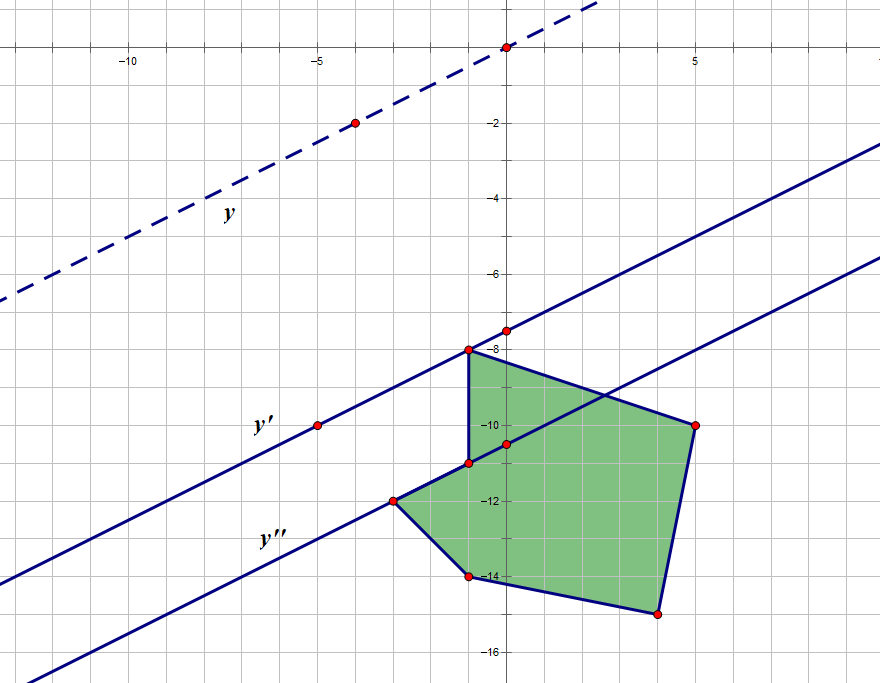
那如果这个图形在函数下面，而我们要让 $b$ 最大呢？

那就往下平移直到第一次碰到多边形的顶点。如图，$y’$ 优于 $y’’$。

例题一

「SDOI2012」任务安排

斜率优化不太好单独讲，所以我把它放在了一道题里。

1.0 版本

数据范围：$1\le n\le 300,0\le S\le 50,1\le T_i,C_i\le 100$。

时间复杂度：$\Theta(n^3)$

最朴素的方法，设 $dp_{i,j}$ 为完成了前 $i$ 个任务，且这 $i$ 个任务被分成了 $j$ 批时的最小费用。状态转移的时候里面再枚举一层 $k$，代表第 $j$ 批任务包含 $k\sim i$ 这些任务。可以列出这个状态转移方程（$sc$ 为 $c$ 的前缀和，$st$ 为 $t$ 的前缀和）：

  • $j\times S+st_i$：这是 $1\sim i$ 任务完成的总时间，注意因为每一批任务执行前都有一个待机时间 $S$，所以需要加上 $j\times S$。
  • $sc_i-sc_{k-1}$：这是第 $j$ 批任务的总费用系数。

2.0 版本

数据范围：$1\le n\le 5000,0\le S\le 50,1\le T_i,C_i\le 100$。

时间复杂度：$\Theta(n^2)$

观察一下 1.0 版本的状态转移方程会发现，如果不是有待机时间的话，$j$ 这一维完全可以省略掉。于是优化的思路呼之欲出了。

虽然我们不能去掉待机时间所带来的费用增加，但是我们可以在每一次分组的时候把后面的所有任务因为这一批的待机时间而产生的费用先计算好加在答案里啊！这样我们就没有必要在计算每一批任务因为前面的待机时间产生的费用了，也就不需要 $j$ 这一维了。也就是说，我们把每个任务的等待时间分成两个部分：前面任务待机时的时间和正在执行任务的时间，分别计算。待机的那一部分时间被我们提前加到答案里，这就是费用提前思想。

设 $dp_i$ 为完成了前 $i$ 个任务时的最小费用。里面枚举一层 $j$，代表最近的这一批任务是 $j+1\sim i$。

于是得出状态转移方程：

  • $S\times (sc_n-sc_j)$：$j+1\sim n$ 这些任务因为 $j+1\sim i$ 这一批任务有等待时间而额外多出来的等待时间，乘上费用系数之和就是这一次等待产生的额外费用。
  • $st_i\times (sc_i-sc_j)$ 因前面所有的任务执行需要耗费时间，$j+1\sim i$ 这一批任务需要等待而产生的费用。这一部分不用提前加上，因为每一次计算中，$st_i$ 都可以包括当前枚举到的任务及之前所有的任务执行的时间。

于是我们就可以愉快地切掉弱化版的 P2365 了。

3.0 版本

数据范围：$1\le n\le 10^4,0\le S\le 50,1\le T_i,C_i\le 100$。

时间复杂度：$\Theta(n)$

可以在状态转移方程的基础上假设 $\bf{j}$ 已经确定，对此方程进行变形。

初始状态：

$dp_i=\min\limits_{j=0}^{i-1}\{dp_j+S\times (sc_n-sc_j)+st_i\times (sc_i-sc_j)\}$

先把 $\min$ 去掉（也就是说这一步我们假设 $j$ 已经确定了）：

$dp_i=dp_j+S\times (sc_n-sc_j)+st_i\times (sc_i-sc_j)$

再把括号拆了：

$dp_i=dp_j+S\times sc_n-S\times sc_j+st_i\times sc_i-st_i\times sc_j$

再移项，把 $dp_j$ 放在左边，$dp_i$ 放在右边，发现右边只有 $sc_j$ 与 $j$ 有关，就把它单独拿出来，剩下的放后面：

$-dp_j=(-S-st_i)\times sc_j-dp_i+S\times sc_n+st_i\times sc_i$

最后把负号去掉，就得到了我们需要的式子：

$dp_j=(S+st_i)\times sc_j+dp_i-S\times sc_n-st_i\times sc_i$

这个式子有啥用呢？如果我们把 $sc_j$ 看成自变量（$x$），$dp_j$ 看成因变量（$y$），就会发现这个式子，它是个一次函数：

对于 2.0 版本的 DP 来说，$dp_i$ 的状态由 $dp_j$ 转移而来，所以在确定 $j$ 之前 $dp_i$ 的值都是不确定的。而斜率优化的时候外层循环变量是 $i$，也就意味着此时 $i$ 确定了但 $j$ 没有确定，所以 $k$ 就定下来了，$b$ 中除了 $dp_i$ 之外也都定下来了，这时我们只需要找到使得 $b$ 最小的 $j$，$dp_i$ 也就取到了最小值。

那什么时候 $b$ 取到最小值呢？利用数形结合，我们可以以 $j$ 为横坐标，$dp_j$ 为纵坐标，把横坐标相差 $1$ 的点两两相连，画出一个图形：

Ps. 为了方便操作，这张图里两个点之间横坐标不一定相差为 $\bf{1}$，但是真实情况每两个点之间横坐标相差为 $\bf{1}$。

这个时候“引入”里面的东西就派上了用场：因为我们要求 $dp_i$ 也就是 $b$ 的最小值，我们只需要从 $b=0$ 开始，把这个一次函数往上移，直到这个函数第一次碰到某一个点为止，这个点就是我们要找的 $j$。

那么，这个点该怎么求呢？

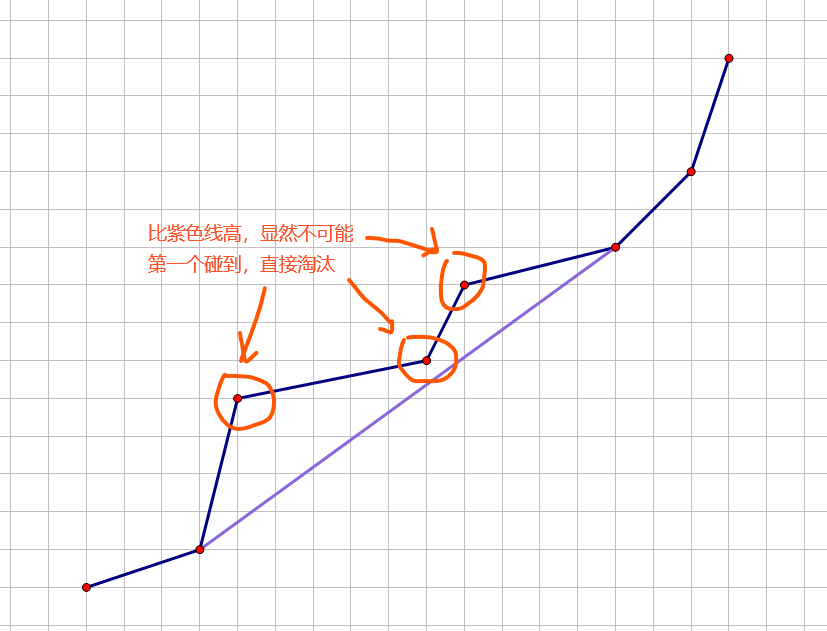
首先有一些点，一看就不可能成为候选，如图：

怎么判断这样的点呢？首先看到点 $3$ 和点 $5$，这两个点的情况比较好分析。就拿点 $3$ 来说，很明显发现 $k_b>k_c$，也就是说这个点“凹下去了”，在函数平移的时候会被旁边“凸起来的”点“挡住”。点 $5$ 同理。

而对于点 $4$，虽然 $k_c<k_d$，但当点 $3$ 和点 $5$ 淘汰之后，把 $(2,4)$ 和 $(4,6)$ 连起来就会发现：

$k_{(2,4)}>k_{(4,6)}$，所以点 $4$ 也没了。

在程序中，显然不能用这种方式来找，而是用每次加入新点时往前逐个淘汰的方式。使用单调队列存点集，从队头到队尾点的横坐标依次增大。每一次 $dp_i$ 算出来之后也要作为新的点加进去，那在加进去之前就在队尾判断，如果把点 $i$ 加进去之后队尾这个点会被淘汰，就把这个点从队尾弹出去，直到队尾符合要求或是队列里没有点了，再把点 $i$ 加进去。

就这样，我们一边加点一边淘汰，导致每一次找 $j$ 的时候图形都是长这样的：

这个图形中每一个顶点都是凸出来的，所以这玩意儿叫做凸包。如果它是往下凸的就叫下凸包，如果是往上凸的就叫上凸包。

所以说了半天，这些凸出来的点到底哪一个才是 $j$？其实对于 $j$ 有一个规律：就是以 $j$ 为右端点的那条线段斜率小于 $k$，而以它为左端点的那条线段斜率大于等于 $k$。

就 3.0 版本数据而言，每一次 $k$ 都不会比上一次小，那么如果前面找到有一条线段的斜率小于当时的 $k$，那在后面，它的斜率也不会比 $k$ 大。对于这种线段我们可以直接把它的左端点从队头弹出单调队列。每一次寻找 $j$ 之前就把这类点弹了，那么此时单调队列的队头就是 $j$。

最后用 $i$ 和 $j$ 状态转移即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <cstdio>
#define ll long long
#define rep(i, j, k) for(int i = j; i <= k; ++i)
#define dep(i, j, k) for(int i = j; i >= k; --i)

const int maxn = (int)1e4 + 5;

int n, s, t[maxn], c[maxn];
ll dp[maxn], st[maxn], sc[maxn];
int L, R, q[maxn];

// y = kx + b
inline ll y(int i) { return dp[i]; }
inline ll k(int i) { return s + st[i]; }
inline ll x(int i) { return sc[i]; }

int main() {
    scanf("%d %d", &n, &s);
    rep(i, 1, n)
        scanf("%d %d", &t[i], &c[i]);
    rep(i, 1, n) {
        st[i] = st[i - 1] + t[i];
        sc[i] = sc[i - 1] + c[i];
    }
    rep(i, 1, n) {
        while(L < R && (y(q[L + 1]) - y(q[L])) < (x(q[L + 1]) - x(q[L])) * k(i))
            ++L;
        dp[i] = dp[q[L]] + st[i] * (sc[i] - sc[q[L]]) + s * (sc[n] - sc[q[L]]);
        while(L < R && (y(i) - y(q[R])) * (x(q[R]) - x(q[R - 1])) <= (y(q[R]) - y(q[R - 1])) * (x(i) - x(q[R])))
            --R;
        q[++R] = i;
    }
    printf("%lld", dp[n]);
    return 0;
}

4.0 版本

数据范围：除了 $T_i$ 可以为负数之外，数据范围与 3.0 版本相同。

时间复杂度：$\Theta(n\log n)$

虽然但是，完成一个任务的时间可以为负数确实挺离谱的。

斜率可以是负数带来了一个问题，就是我们不能在用左端点淘汰的方式直接找 $i$ 了。

为啥呢？因为左端点淘汰有一个条件，就是因为被淘汰的点回不来，所以每一次 $k$ 都不能比上一次小。$T_i>0$ 时 $st$ 肯定是递增的，但是现在不一定了，这也就意味着 $k$ 可能会变小，那对于之前因为所在线段斜率小于当时的 $k$ 而被淘汰的点，但是这条线段的斜率大于现在的这个 $k$，那这个点是不是还要回来？这个很明显就乱套了。

不过我们还有其它的方法。

因为就算斜率可以是负数，$k$ 的单调性没了，但凸包单调性依然存在。所以一种时间复杂度劣一点，但是适用于负数的方法出现了——二分。

二分查找第一个斜率大于 $k$ 的线段，它的左端点就是 $i$。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>
#define ll long long
#define rep(i, j, k) for(int i = j; i <= k; ++i)
#define dep(i, j, k) for(int i = j; i >= k; --i)

const int maxn = (int)3e5 + 5;

int n, s, t[maxn], c[maxn], st[maxn], sc[maxn];
ll dp[maxn];
int L, R, q[maxn];

// y = kx + b
inline ll y(int i) { return dp[i]; }
inline ll k(int i) { return s + st[i]; }
inline ll x(int i) { return sc[i]; }

inline int f(int l, int r, int i) {
    if(l == r)
        return l;
    int mid = (l + r) >> 1;
    if(y(q[mid + 1]) - y(q[mid]) < (x(q[mid + 1]) - x(q[mid])) * i)
        return f(mid + 1, r, i);
    return f(l, mid, i);
}

int main() {
    scanf("%d %d", &n, &s);
    rep(i, 1, n)
        scanf("%d %d", &t[i], &c[i]);
    rep(i, 1, n) {
        st[i] = st[i - 1] + t[i];
        sc[i] = sc[i - 1] + c[i];
    }
    int j;
    rep(i, 1, n) {
        j = q[f(L, R, k(i))];
        dp[i] = dp[j] + st[i] * 1ll * (sc[i] - sc[j]) + s * 1ll * (sc[n] - sc[j]);
        while(L < R && (y(i) - y(q[R])) * (x(q[R]) - x(q[R - 1])) <= (y(q[R]) - y(q[R - 1])) * (x(i) - x(q[R])))
            --R;
        q[++R] = i;
    }
    printf("%lld", dp[n]);
    return 0;
}

Ps. 注意精度的问题，计算斜率的除法需要转换为乘法。

斜率优化大概就是 3.0 版本那个样子，4.0 是对斜率优化普适性的一种优化。

例题二

「SDOI2016」征途

我和 XSC062 研究这道题研究了半天，最后发现 mjl 和 gm 讲斜优完全讲的是两个东西。

首先是前置工作：

$
p=\dfrac{a_1+a_2+\ldots+a_m}{m}
\
v=\dfrac{(a_1-p)^2+(a_2-p)^2+\ldots+(a_m-p)^2}{m}
$

$(\sum\limits_{i=1}^m a_i)^2$ 是个常数，所以 $dp$ 应该求的是 $m\times(a_1^2+a_2^2+\ldots+a_m^2)$ 的最小值。

设 $dp_{i,j}$ 为走了 $i$ 天之后，走了 $j$ 段的最小的那个值。状态转移的时候再套一层 $k$，表示第 $i$ 天走了 $k+1\sim j$ 这些路段。

很容易可以得到状态转移方程（$sum$ 数组是 $a$ 的前缀和）：

好了，接下来就是重头戏：怎么斜率优化？

首先要确定这三个循环变量哪一个作为自变量 $x$，这不是随便选的，观察一下这个状态转移方程就会发现有一个 $(sum_j-sum_k)^2$ 展开之后是 $sum_j^2+sum_k^2-2\times sum_j\times sum_k$，这个东西比较难处理，不过有一个 $2\times sum_j\times sum_k$ 作为切入点，所以我们选择 $k$ 作为自变量 $x$，这样 $2\times sum_j$ 就作为斜率 $k$，$sum_j^2$ 就作为 $b$ 的一部分，比较难处理的 $sum_k^2$ 就挪到等号左边作为 $y$ 的一部分。因为斜率优化之后也要枚举自变量的值，所以说 $sum_k^2$ 不会影响最后的结果。

由于是求最小值，所以维护下凸包。然后就是板子了。